Group: defining topological entitiesFunction: defining global and piecewise expressionsConstraint: specifying constraints on function spaces and formulationsFunctionSpace: building function spacesJacobian: defining jacobian methodsIntegration: defining integration methodsFormulation: building equationsResolution: solving systems of equationsPostProcessing: exploiting computational resultsPostOperation: exporting resultsGroup examplesFunction examplesConstraint examplesFunctionSpace examples
Jacobian examplesIntegration examplesFormulation examples
Resolution examples
PostProcessing examplesPostOperation examplesNext: Obtaining GetDP, Previous: (dir), Up: (dir) [Contents][Index]
Patrick Dular and Christophe Geuzaine
GetDP is a general finite element solver that uses mixed finite elements to discretize de Rham-type complexes in one, two and three dimensions. This is the GetDP Reference Manual for GetDP 3.5.0 (May 13, 2022).
| • Obtaining GetDP | ||
| • Copying conditions | Terms and conditions of use. | |
| • Overview | What is GetDP? | |
| • How to Read this Manual | Which parts of this manual should you read? | |
| • Running GetDP | How to run GetDP on your machine. | |
| • Expressions | Definition of basic expressions in GetDP. | |
| • Objects | Definition of the 10 GetDP objects. | |
| • Types for objects | Definition of all available types for the 10 objects. | |
| • Short examples | Simple object examples. | |
| • Complete examples | Some simple complete examples. | |
| • File formats | Input and output file formats. | |
| • Gmsh examples | Sample Gmsh input files. | |
| • Compiling the source code | Information on how to comile GetDP from source | |
| • Frequently asked questions | The GetDP FAQ | |
| • Tips and tricks | Some tips to make your life easier with GetDP. | |
| • Version history | Changelog | |
| • Copyright and credits | Copyright information and list of contributors | |
| • License | Complete copy of the license. | |
| • Concept index | Index of concepts. | |
| • Metasyntactic variable index | Index of metasyntactic variables used in this manual. | |
| • Syntax index | Index of reserved keywords in the GetDP language. | |
Next: Copying conditions, Previous: Top, Up: Top [Contents][Index]
The source code and various pre-compiled versions of GetDP (for Windows, Linux and MacOS) can be downloaded from http://getdp.info.
If you use GetDP, we would appreciate that you mention it in your work. References and the latest news about GetDP are always available on http://getdp.info.
Next: Overview, Previous: Obtaining GetDP, Up: Top [Contents][Index]
GetDP is “free software”; this means that everyone is free to use it and to redistribute it on a free basis. GetDP is not in the public domain; it is copyrighted and there are restrictions on its distribution, but these restrictions are designed to permit everything that a good cooperating citizen would want to do. What is not allowed is to try to prevent others from further sharing any version of GetDP that they might get from you.
Specifically, we want to make sure that you have the right to give away copies of GetDP, that you receive source code or else can get it if you want it, that you can change GetDP or use pieces of GetDP in new free programs, and that you know you can do these things.
To make sure that everyone has such rights, we have to forbid you to deprive anyone else of these rights. For example, if you distribute copies of GetDP, you must give the recipients all the rights that you have. You must make sure that they, too, receive or can get the source code. And you must tell them their rights.
Also, for our own protection, we must make certain that everyone finds out that there is no warranty for GetDP. If GetDP is modified by someone else and passed on, we want their recipients to know that what they have is not what we distributed, so that any problems introduced by others will not reflect on our reputation.
The precise conditions of the license for GetDP are found in the General Public License that accompanies the source code (see License). Further information about this license is available from the GNU Project webpage http://www.gnu.org/copyleft/gpl-faq.html. Detailed copyright information can be found in Copyright and credits.
If you want to integrate parts of GetDP into a closed-source software, or want to sell a modified closed-source version of GetDP, you will need to obtain a different license. Please contact us directly for more information.
Next: How to Read this Manual, Previous: Copying conditions, Up: Top [Contents][Index]
GetDP (a “General environment for the treatment of Discrete Problems”) is a scientific software environment for the numerical solution of integro-differential equations, open to the coupling of physical problems (electromagnetic, thermal, etc.) as well as of numerical methods (finite element method, integral methods, etc.). It can deal with such problems of various dimensions (1D, 2D or 3D) and time states (static, transient or harmonic).
The main feature of GetDP is the closeness between its internal structure (written in C), the organization of data defining discrete problems (written by the user in ASCII data files) and the symbolic mathematical expressions of these problems. Its aim is to be welcoming and of easy use for both development and application levels: it consists of a working environment in which the definition of any problem makes use of a limited number of objects, which makes the environment structured and concise. It therefore gives researchers advanced developing tools and a large freedom in adding new functionalities.
The modeling tools provided by GetDP can be tackled at various levels of complexity: this opens the software to a wide range of activities, such as research, collaboration, education, training and industrial studies.
| • Numerical tools as objects | ||
| • Which problems can GetDP actually solve? | ||
| • Bug reports |
Next: Which problems can GetDP actually solve?, Previous: Overview, Up: Overview [Contents][Index]
An assembly of computational tools (or objects) in GetDP leads to a problem definition structure, which is a transcription of the mathematical expression of the problem, and forms a text data file: the equations describing a phenomenon, written in a mathematical form adapted to a chosen numerical method, directly constitute data for GetDP.
The resolution of a discrete problem with GetDP requires the definition, in a text data file, of the GetDP objects listed (together with their dependencies) in the following figure and table.
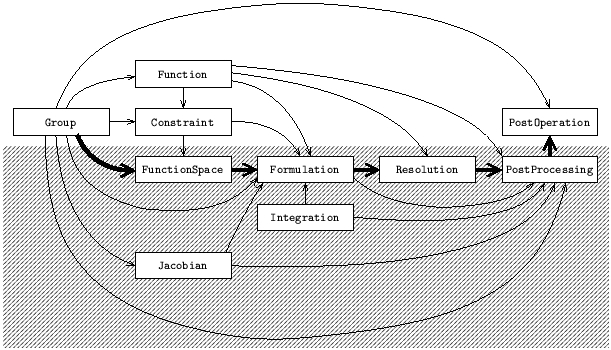
Group ---
Function Group
Constraint Group, Function, (Resolution)
FunctionSpace Group, Constraint, (Formulation), (Resolution)
Jacobian Group
Integration ---
Formulation Group, Function, (Constraint), FunctionSpace,
Jacobian, Integration
Resolution Function, Formulation
PostProcessing Group, Function, Jacobian, Integration,
Formulation, Resolution
PostOperation Group, PostProcessing
The gathering of all these objects constitutes the problem definition structure, which is a copy of the formal mathematical formulation of the problem. Reading the first column of the table from top to bottom pictures the working philosophy and the linking of operations peculiar to GetDP, from group definition to results visualization. The decomposition highlighted in the figure points out the separation between the objects defining the method of resolution, which may be isolated in a “black box” (bottom) and those defining the data peculiar to a given problem (top).
The computational tools which are in the center of a problem definition
structure are formulations (Formulation) and function spaces
(FunctionSpace). Formulations define systems of equations that have
to be built and solved, while function spaces contain all the quantities,
i.e., functions, fields of vectors or covectors, known or not, involved in
formulations.
Each object of a problem definition structure must be defined before
being referred to by others. A linking which always respects this
property is the following: it first contains the objects defining
particular data of a problem, such as geometry, physical characteristics
and boundary conditions (i.e., Group, Function and
Constraint) followed by those defining a resolution method, such
as unknowns, equations and related objects (i.e., Jacobian,
Integration, FunctionSpace, Formulation,
Resolution and PostProcessing). The processing cycle ends
with the presentation of the results (i.e., lists of numbers in various
formats), defined in PostOperation fields. This decomposition
points out the possibility of building black boxes, containing objects
of the second group, adapted to treatment of general classes of problems
that share the same resolution methods.
Next: Bug reports, Previous: Numerical tools as objects, Up: Overview [Contents][Index]
The preceding explanations may seem very (too) general. Which are the problems that GetDP can actually solve? To answer this question, here is a list of methods that we have considered and coupled until now:
finite element method
boundary element method (experimental, undocumented)
volume integral methods (experimental, undocumented)
one-dimensional models (1D)
two-dimensional models (2D), plane and axisymmetric
three-dimensional models (3D)
static states
sinusoidal and harmonic states
transient states
eigenvalue problems
These methods have been successfully applied to build coupled physical models involving electromagnetic phenomena (magnetostatics, magnetodynamics, electrostatics, electrokinetics, electrodynamics, wave propagation, lumped electric circuits), acoustic phenomena, thermal phenomena and mechanical phenomena (elasticity, rigid body movement).
As can be guessed from the preceding list, GetDP has been initially developed in the field of computational electromagnetics, which fully uses all the offered coupling features. We believe that this does not interfere with the expected generality of the software because a particular modeling forms a problem definition structure which is totally external to the software: GetDP offers computational tools; the user freely applies them to define and solve his problem.
Nevertheless, specific numerical tools will always need to be implemented to solve specific problems in areas other than those mentionned above. If you think the general phisosophy of GetDP is right for you and your problem, but you discover that GetDP lacks the tools necessary to handle it, let us know: we would love to discuss it with you. For example, at the time of this writing, many areas of GetDP would need to be improved to make GetDP as useful for computational mechanics or computational fluid dynamics as it is for computational electromagnetics... So if you have the skills and some free time, feel free to join the project: we gladly accept all code contributions!
Previous: Which problems can GetDP actually solve?, Up: Overview [Contents][Index]
Please file issues on https://gitlab.onelab.info/getdp/getdp/issues. Provide as precise a description of the problem as you can, including sample input files that produce the bug. Don’t forget to mention both the version of GetDP and the version of your operation system (see Running GetDP to see how to get this information).
See Frequently asked questions, and the bug tracking system to see which problems we already know about.
Next: Running GetDP, Previous: Overview, Up: Top [Contents][Index]
After reading Overview, which depicts the general philosophy of GetDP, you might want to skip Expressions, Objects and Types for objects and directly run the demo files bundled in the distribution on your computer (see Running GetDP). You should then open these examples with a text editor and compare their structure with the examples given in Short examples and Complete examples. For each new syntax element that you fall onto, you can then go back to Expressions, Objects, and Types for objects, and find in these chapters the detailed description of the syntactic rules as well as all the available options.
Indexes for many concepts (see Concept index) and for all the syntax elements (see Syntax index) are available at the end of this manual.
| • Syntactic rules |
Previous: How to Read this Manual, Up: How to Read this Manual [Contents][Index]
Here are the rules we tried to follow when writing this user’s guide. Note that metasyntactic variable definitions stay valid throughout all the manual (and not only in the sections where the definitions appear). See Metasyntactic variable index, for an index of all metasyntactic variables.
this.
:) after a metasyntactic variable separates the variable
from its definition.
< > pairs.
|.
rule <, rule > …
is replaced by rule <,…>.
Next: Expressions, Previous: How to Read this Manual, Up: Top [Contents][Index]
GetDP has no graphical interface1. It is a command-line driven program that reads a problem definition file once at the beginning of the processing. This problem definition file is a regular ASCII text file (see Numerical tools as objects), hence created with whatever text editor you like.
If you just type the program name at your shell prompt (without any argument), you will get a short help on how to run GetDP. All GetDP calls look like
getdp filename options
where filename is the ASCII file containing the problem definition, i.e., the structures this user’s guide has taught you to create. This file can include other files (see Includes), so that only one problem definition file should always be given on the command line. The input files containing the problem definition structure are usually given the .pro extension (if so, there is no need to specify the extension on the command line). The name of this file (without the extension) is used as a basis for the creation of intermediate files during the pre-processing and the processing stages.
The options are a combination of the following commands (in any order):
-pre
resolution-id
Performs the pre-processing associated with the resolution resolution-id. In the pre-processing stage, GetDP creates the geometric database (from the mesh file), identifies the degrees of freedom (the unknowns) of the problem and sets up the constraints on these degrees of freedom. The pre-processing creates a file with a .pre extension. If resolution-id is omitted, the list of available choices is displayed.
-cal
Performs the processing. This requires that a pre-processing has been
performed previously, or that a -pre option is given on the same
command line. The performed resolution is the one given as an argument to
the -pre option. In the processing stage, GetDP executes all the
commands given in the Operation field of the selected
Resolution object (such as matrix assemblies, system resolutions,
…).
-pos
post-operation-id …
Performs the operations in the PostOperation(s) selected by the
post-operation-id(s). This requires that a processing has been
performed previously, or that a -cal option is given on the same
command line. If post-operation-id is omitted, the list of available
choices is displayed.
-msh
filename
Reads the mesh (in .msh format) from filename (see File formats) rather than from the default problem file name (with the
.msh extension appended).
-msh_scaling
value
Multiplies the coordinates of all the nodes in the mesh by value.
-gmshread
filename …
Read gmsh data files (same as GmshRead in Resolution
operations). Allows to use such datasets outside resolutions (e.g. in
pre-processing).
-split
Saves processing results in separate files (one for each timestep).
-res
filename …
Loads processing results from file(s).
-name
string
Uses string as the default generic file name for input or output of mesh, pre-processing and processing files.
-restart
Restarts processing of a time stepping resolution interrupted before being complete.
-solve
resolution-id
Same as -pre resolution-id -cal.
-solver
filename
Specifies a solver option file (whose format varies depending on the linear algebra toolkit used).
-slepc
Uses SLEPc instead of Arpack as eigensolver.
-adapt
file
Reads adaptation constraints from file.
-order
real
Specifies the maximum interpolation order.
-cache
Caches network computations to disk.
-bin
Selects binary format for output files.
-v2
Creates mesh-based Gmsh output files when possible.
-check
Lets you check the problem structure interactively.
-v
-verbose
integer
Sets the verbosity level. A value of 0 means that no information will be displayed during the processing.
-cpu
Reports CPU times for all operations.
-p
-progress
integer
Sets the progress update rate. This controls the refreshment rate of the counter indicating the progress of the current computation (in %).
-onelab
name <address>
Communicates with OneLab (file or server address)
-setnumber
name value
Sets constant number name to value
-setstring
name value
Sets constant string name to value
-info
Displays the version information.
-version
Displays the version number.
-help
Displays a message listing basic usage and available options.
Next: Objects, Previous: Running GetDP, Up: Top [Contents][Index]
This chapter and the next two describe in a rather formal way all the commands that can be used in the ASCII text input files. If you are just beginning to use GetDP, or just want to see what GetDP is all about, you should skip this chapter and the next two for now, have a quick look at Running GetDP, and run the demo problems bundled in the distribution on your computer. You should then open the .pro files in a text editor and compare their structure with the examples given in Short examples and Complete examples. Once you have a general idea of how the files are organized, you might want to come back here to learn more about the specific syntax of all the objects, and all the available options.
| • Comments | ||
| • Includes | ||
| • Expression definition | ||
| • Constants | ||
| • Operators | ||
| • Functions | ||
| • Current values | ||
| • Arguments | ||
| • Run-time variables and registers | ||
| • Fields | ||
| • Macros loops and conditionals |
Next: Includes, Previous: Expressions, Up: Expressions [Contents][Index]
Both C and C++ style comments are supported and can be used in the input data files to comment selected text regions:
/* and */ pairs is ignored;
// is ignored.
Comments cannot be used inside double quotes or inside GetDP keywords.
Next: Expression definition, Previous: Comments, Up: Expressions [Contents][Index]
An input data file can be included in another input data file by placing one of the following commands (expression-char represents a file name) on a separate line, outside the GetDP objects. Any text placed after an include command on the same line is ignored.
Include expression-char#include expression-char
See Constants, for the definition of the character expression expression-char.
Next: Constants, Previous: Includes, Up: Expressions [Contents][Index]
Expressions are the basic tool of GetDP. They cover a wide range of functional expressions, from constants to formal expressions containing functions (built-in or user-defined, depending on space and time, etc.), arguments, discrete quantities and their associated differential operators, etc. Note that ‘white space’ (spaces, tabs, new line characters) is ignored inside expressions (as well as inside all GetDP objects).
Expressions are denoted by the metasyntactic variable expression (remember the definition of the syntactic rules in Syntactic rules):
expression:
( expression ) |
integer |
real |
constant-id |
quantity |
argument |
current-value |
variable-set |
variable-get |
register-set |
register-get |
operator-unary expression |
expression operator-binary expression |
expression operator-ternary-left expression operator-ternary-right expression |
built-in-function-id [ < expression-list > ] < { expression-cst-list } > |
function-id [ < expression-list > ] |
< Real | Complex > [ expression ] |
Dt [ expression ] |
AtAnteriorTimeStep [ expression, integer ] |
Order [ quantity ] |
Trace [ expression, group-id ] |
expression ##integer
The following sections introduce the quantities that can appear in expressions, i.e., constant terminals (integer, real) and constant expression identifiers (constant-id, expression-cst-list), discretized fields (quantity), arguments (argument), current values (current-value), register values (register-set, register-get), operators (operator-unary, operator-binary, operator-ternary-left, operator-ternary-right) and built-in or user-defined functions (built-in-function-id, function-id). The last seven cases in this definition permit to cast an expression as real or complex, get the time derivative or evaluate an expression at an anterior time step, retrieve the interpolation order of a discretized quantity, evaluate the trace of an expression, and print the value of an expression for debugging purposes.
List of expressions are defined as:
expression-list: expression <,…>
| • Operators | ||
| • Constants | ||
| • Functions | ||
| • Current values | ||
| • Fields |
Next: Operators, Previous: Expression definition, Up: Expressions [Contents][Index]
The three constant types used in GetDP are integer, real and string. These types have the same meaning and syntax as in the C or C++ programming languages. Besides general expressions (expression), purely constant expressions, denoted by the metasyntactic variable expression-cst, are also used:
expression-cst:
( expression-cst ) |
integer |
real |
constant-id |
operator-unary expression-cst |
expression-cst operator-binary expression-cst |
expression-cst operator-ternary-left expression-cst operator-ternary-right
expression-cst |
math-function-id [ < expression-cst-list > ] |
#constant-id() |
constant-id(expression-cst) |
StrFind[ expression-char, expression-char ] |
StrCmp[ expression-char, expression-char ] |
StrLen[ expression-char ] |
StringToName[ expression-char ] | S2N[ expression-char ] |
Exists[ string ] | FileExists[ string ] | GroupExists[ string ] |
GetForced[ string ] | NbrRegions [ string ] |
GetNumber[ expression-char <, expression-cst> ]
StrFind searches the first expression-char for any
occurrence of the second expression-char. StrCmp compares
the two strings (returns an integer greater than, equal to, or less than
0, according as the first string is greater than, equal to, or less than
the second string). StrLen returns the length of the
string. StringToName creates a name from the provided
string. Exists checks for the existence of a constant or a
function. FileExists checks for the existence of a
file. GroupExists checks for the existence of a
group. GetForced gets the value of a constant (zero if does not
exist). NbrRegions counts the numbers of elementary regions in a
group. GetNumber allows to get the value of a ONELAB number
variable (the optional second argument specifies the default value
returned if the variable does not exist).
List of constant expressions are defined as:
expression-cst-list: expression-cst-list-item <,…>
with
expression-cst-list-item:
expression-cst |
expression-cst : expression-cst |
expression-cst : expression-cst : expression-cst |
constant-id () |
constant-id ( { expression-cst-list } ) |
List[ constant-id ] |
List[ expression-cst-list-item ] |
List[ { expression-cst-list } ] |
ListAlt[ constant-id, constant-id ] |
ListAlt[ expression-cst-list-item, expression-cst-list-item ] |
LinSpace[ expression-cst, expression-cst, expression-cst ] |
LogSpace[ expression-cst, expression-cst, expression-cst ] |
- expression-cst-list-item |
expression-cst * expression-cst-list-item |
expression-cst-list-item * expression-cst |
expression-cst / expression-cst-list-item |
expression-cst-list-item / expression-cst |
expression-cst-list-item ^ expression-cst |
expression-cst-list-item + expression-cst-list-item |
expression-cst-list-item - expression-cst-list-item |
expression-cst-list-item * expression-cst-list-item |
expression-cst-list-item / expression-cst-list-item |
ListFromFile [ expression-char ] |
ListFromServer [ expression-char ]
The second case in this last definition permits to create a list
containing the range of numbers comprised between the two
expression-cst, with a unit incrementation step. The third case
also permits to create a list containing the range of numbers comprised
between the two expression-cst, but with a positive or negative
incrementation step equal to the third expression-cst. The fourth
and fifth cases permit to reference constant identifiers
(constant-ids) of lists of constants and constant identifiers of
sublists of constants (see below for the definition of constant
identifiers) . The sixth case is a synonym for the fourth. The seventh
case permits to create alternate lists: the arguments of ListAlt
must be constant-ids of lists of constants of the same
dimension. The result is an alternate list of these constants: first
constant of argument 1, first constant of argument 2, second constant of
argument 1, etc. These kinds of lists of constants are for example often
used for function parameters (see Functions). The next two cases
permit to create linear and logarithmic lists of numbers,
respectively. The remaining cases permit to apply arithmetic operators
item-wise in lists. ListFromFile reads a list of numbers from a
file. ListFromServer attemps to get a list of numbers from the
ONELAB variable expression-char.
Contrary to a general expression which is evaluated at runtime (thanks to an internal stack mechanism), an expression-cst is completely evaluated during the syntactic analysis of the problem (when GetDP reads the .pro file). The definition of such constants or lists of constants with identifiers can be made outside or inside any GetDP object. The syntax for the definition of constants is:
affectation:
DefineConstant [ constant-id < = expression-cst > <,…> ]; |
DefineConstant [ constant-id = { expression-cst , onelab-options } <,…> ]; |
DefineConstant [ string-id < = string-def > <,…> ]; |
DefineConstant [ string-id = { string-def , onelab-options } <,…> ]; |
constant-id <()> = constant-def; |
constant-id = DefineNumber[ constant-def, onelab-options ];
string-id <()> = string-def; |
string-id = DefineString[ string-def, onelab-options ]; |
Printf [ "string" ] < > | >> string-def >; |
Printf [ "string", expression-cst-list ] < > | >> string-def >; |
Read [ constant-id ] ; |
Read [ constant-id , expression-cst ]; |
UndefineConstant | Delete [ constant-id ] ;
UndefineFunction [ constant-id ] ;
SetNumber[ string , expression-cst ];
SetString[ string , string-def ];
with
constant-id:
string |
string ( expression-cst-list ) |
string ~ { expression-cst } <,…>
constant-def:
expression-cst-list-item |
{ expression-cst-list }
string-id:
string |
string ~ { expression-cst } <,…>
string-def:
"string" |
StrCat[ expression-char <,…> ] |
Str[ expression-char <,…> ]
Notes:
Pi (3.1415926535897932),
0D (0), 1D (1), 2D (2) and 3D (3).
~{expression-cst} is appended to a string string,
the result is a new string formed by the concatenation of string,
_ (an underscore) and the value of the expression-cst. This is
most useful in loops (see Macros loops and conditionals), where it permits to
define unique strings automatically. For example,
For i In {1:3}
x~{i} = i;
EndFor
is the same as
x_1 = 1; x_2 = 2; x_3 = 3;
DefineConstant (zero if no expression-cst is
given) is performed only if constant-id has not yet been defined. This
kind of explicit default definition mechanism is most useful in general
problem definition structures making use of a large number of generic
constants, functions or groups. When exploiting only a part of a complex
problem definition structure, the default definition mechanism allows to
define the quantities of interest only, the others being assigned a default
value (that will not be used during the processing but that avoids the error
messages produced when references to undefined quantities are made).
When onelab-options are provided, the parameter is exchanged with the ONELAB server. See https://gitlab.onelab.info/doc/tutorials/wikis/ONELAB-syntax-for-Gmsh-and-GetDP for more information.
DefineNumber and DefineString allow to define a ONELAB
parameter. In this case the affectation always takes
place. SetNumber and SetString allow the direct setting of
ONELAB parameters without defining local variables.
See Constant expression examples, as well as Function examples, for some examples.
Character expressions are defined as follows:
expression-char: "string" | string-id | StrCat[ expression-char <,…> ] | Str[ expression-char <,…> ] StrChoice[ expression, expression-char, expression-char ] | StrSub[ expression-char, expression, expression ] | StrSub[ expression-char, expression ] | UpperCase [ expression-char ] | Sprintf [ expression-char ] | Sprintf[ expression-char, expression-cst-list ] | NameToString ( string ) | N2S ( string ) | GetString[ expression-char <, expression-char,> ] | Date | CurrentDirectory | CurrentDir | AbsolutePath [ expression-char ] | DirName [ expression-char ] | OnelabAction
StrCat and Str permit to concatenate
character expressions (Str adds a newline character after each
string except the last) when creating a string. Str is also used
to create string lists (when string-id is followed by
()). StrChoice returns the first or second
expression-char depending on the value of expression.
StrSub returns the portion of the string that starts at the
character position given by the first expression and spans the
number of characters given by the second expression or until the
end of the string (whichever comes first; or always if the second
expression is not provided). UpperCase converts the
expression-char to upper case. Sprintf is equivalent to the
sprintf C function (where expression-char is a format
string that can contain floating point formatting characters: %e,
%g, etc.). NameToString converts a variable name into a
string. GetString allows to get the value of a ONELAB string
variable (the optional second argument specifies the default value
returned if the variable does not exist.) Date permits to access
the current date. CurrentDirectory and CurrentDir return
the directory of the .pro file. AbsolutePath returns the
absolute path of a file. DirName returns the directory of a
file. OnelabAction returns the current ONELAB action
(e.g. check or compute).
List of character expressions are defined as:
expression-char-list: expression-char <,…>
Next: Functions, Previous: Constants, Up: Expressions [Contents][Index]
| • Operator types | ||
| • Evaluation order |
Next: Evaluation order, Previous: Operators, Up: Operators [Contents][Index]
The operators in GetDP are similar to the corresponding operators in the C or C++ programming languages.
operator-unary:
-Unary minus.
!Logical not.
operator-binary:
^Exponentiation. The evaluation of the both arguments must result in a scalar value.
*Multiplication or scalar product, depending on the type of the arguments.
/\Cross product. The evaluation of both arguments must result in vectors.
/Division.
%Modulo. The evaluation of the second argument must result in a scalar value.
+Addition.
-Subtraction.
==Equality.
!=Inequality.
>Greater. The evaluation of both arguments must result in scalar values.
>=Greater or equality. The evaluation of both arguments must result in scalar values.
<Less. The evaluation of both arguments must result in scalar values.
<=Less or equality. The evaluation of both arguments must result in scalar values.
&&Logical ‘and’. The evaluation of both arguments must result in scalar values.
||Logical ‘or’. The evaluation of both arguments must result in floating point
values. Warning: the logical ‘or’ always (unlike in C or C++) implies the
evaluation of both arguments. That is, the second operand of || is
evaluated even if the first one is true.
&Binary ‘and’.
|Binary ‘or’.
>>Bitwise right-shift operator. Shifts the bits of the first argument to the right by the number of bits specified by the second argument.
<<Bitwise left-shift operator. Shifts the bits of the first argument to the left by the number of bits specified by the second argument.
operator-ternary-left:
?operator-ternary-right:
:The only ternary operator, formed by operator-ternary-left and
operator-ternary-right is defined as in the C or C++ programming
languages. The ternary operator first evaluates its first argument (the
expression-cst located before the ?), which must result in a
scalar value. If it is true (non-zero) the second argument (located between
? and :) is evaluated and returned; otherwise the third
argument (located after :) is evaluated and returned.
Previous: Operator types, Up: Operators [Contents][Index]
The evaluation priorities are summarized below (from stronger to weaker,
i.e., ^ has the highest evaluation priority). Parentheses
() may be used anywhere to change the order of evaluation.
^- (unary), !| &/\*, /, %+, -<, >, <=, >=, <<, >>!=, ==&&, ||?:Next: Current values, Previous: Operators, Up: Expressions [Contents][Index]
Two types of functions coexist in GetDP: user-defined functions (function-id, see Function) and built-in functions (built-in-function-id, defined in this section).
Both types of functions are always followed by a pair of brackets []
that can possibly contain arguments (see Arguments). This makes it
simple to distinguish a function-id or a built-in-function-id
from a constant-id. As shown below, built-in functions might also have
parameters, given between braces {}, and which are completely
evaluated during the analysis of the syntax (since they are of
expression-cst-list type):
built-in-function-id [ < expression-list > ] < { expression-cst-list } >
with
built-in-function-id: math-function-id | extended-math-function-id | green-function-id | type-function-id | coord-function-id | misc-function-id
Notes:
Next: Arguments, Previous: Functions, Up: Expressions [Contents][Index]
Current values return the current floating point value of an internal GetDP variable:
$TimeValue of the current time. This value is set to zero for non time dependent analyses.
$DTimeValue of the current time increment used in a time stepping algorithm.
$ThetaCurrent theta value in a theta time stepping algorithm.
$TimeStepNumber of the current time step in a time stepping algorithm.
$BreakpointIn case of a breakpoint hit in TimeLoopAdaptive it is the number of the current breakpoint. In the other case when $Time corresponds not to a breakpoint the value is -1.
$Iteration, $NLIterationCurrent iteration in a nonlinear loop.
$Residual, $NLResidualCurrent residual in a nonlinear loop.
$EigenvalueRealReal part of the current eigenvalue.
$EigenvalueImagImaginary part of the current eigenvalue.
$X, $XSValue of the current (destination or source) X-coordinate.
$Y, $YSValue of the current (destination or source) Y-coordinate.
$Z, $ZSValue of the current (destination or source) Z-coordinate.
$A, $B, $CValue of the current parametric coordinates used in the parametric
OnGrid PostOperation (see Types for PostOperation).
$QuadraturePointIndexIndex of the current quadrature point.
$KSPIterationCurrent iteration in a Krylov subspace solver.
$KSPResidualCurrent residual in a Krylov subspace solver.
$KSPIterationsTotal number of iterations of Krylov subspace solver.
$KSPSystemSizeSystem size of Krylov subspace solver.
Note:
Current values are “read-only”. User-defined run-time variables, which share the same syntax but whose value can be changed in an expression, are defined in Run-time variables and registers.
Next: Run-time variables and registers, Previous: Current values, Up: Expressions [Contents][Index]
Function arguments can be used in expressions and have the following syntax (integer indicates the position of the argument in the expression-list of the function, starting from 1):
argument: $integer
See Function, and Function examples, for more details.
Next: Fields, Previous: Arguments, Up: Expressions [Contents][Index]
Constant expressions (expression-csts) are evaluated only once
during the analysis of the problem definition structure, cf.
Constants. While this is perfectly fine in most situations,
sometimes it is necessary to store and modify variables at run-time. For
example, an iteration in a Resolution could depend on values
computed at run-time. Also, to speed-up the evaluation of
expressions (which are evaluated at runtime through GetDP’s
internal stack mechanism), it can be useful to save some results in a
temporary variable, at run-time, in order to reuse them later on.
Two mechanisms exit to handle such cases: run-time variables (which follow the same syntax as Current values), and registers.
Run-time variables have the following syntax:
variable-set:
$variable-id = expression
variable-get:
$variable-id
variable-id:
string |
string ~ { expression-cst } <,…>
Thus, run-time variables can simply be defined anywhere in an expression and be reused later on. Current values can be seen as special cases of run-time variables, which are read-only.
Registers have the following syntax:
register-set: expression#expression-cst register-get: #expression-cst
Thus, to store any expression in the register 5, one
should add #5 directly after the expression. To reuse the value
stored in this register, one simply uses #5 instead of the
expression it should replace.
See Function examples, for an example.
Next: Macros loops and conditionals, Previous: Run-time variables and registers, Up: Expressions [Contents][Index]
A discretized quantity (defined in a function space, cf.
FunctionSpace) is represented between braces {}, and can only
appear in well-defined expressions in Formulation
(see Formulation) and PostProcessing (see PostProcessing)
objects:
quantity:
< quantity-dof > { < quantity-operator > quantity-id } |
{ < quantity-operator > quantity-id } [ expression-cst-list ]
with
quantity-id:
string |
string ~ { expression-cst }
and
quantity-dof:
Dof
Defines a vector of discrete quantities (vector of Degrees of
freedom), to be used only in Equation terms of formulations to
define (elementary) matrices. Roughly said, the Dof symbol in front
of a discrete quantity indicates that this quantity is an unknown quantity,
and should therefore not be considered as already computed.
An Equation term must be linear with respect to the
Dof. Thus, for example, a nonlinear term like
Integral { [ f[] * Dof{T}^4 , {T} ]; … }
must first be linearized; and while
Integral { [ f[] * Dof{T} , {T} ]; … }
Integral { [ -f[] * 12 , {T} ]; … }
is valid, the following, which is affine but not linear, is not:
Integral { [ f[] * (Dof{T} - 12) , {T} ]; … }
GetDP supports two linearization techniques. The first is functional
iteration (or Picard method), where one simply plugs the value obtained
at the previous iteration into the nonlinear equation (the previous
value is known, and is accessed e.g. with {T} instead
Dof{T}). The second is the Newton-Raphson iteration, where the
Jacobian is specified with a JacNL equation term.
BF
Indicates that only a basis function will be used (only valid with basis functions associated with regions).
quantity-operator:
d
Exterior derivative (d): applied to a p-form, gives a (p+1)-form.
Grad
Gradient: applied to a scalar field, gives a vector.
Curl
Rot
Curl: applied to a vector field, gives a vector.
Div
Divergence (div): applied to a vector field, gives a scalar.
D1
Applies the operator specified in the first argument of dFunction
{ basis-function-type, basis-function-type }
(see FunctionSpace). This is currently only used for
nodal-interpolated vector fields (interpolated with BF_Node_X,
BF_Node_Y, BF_Node_Z)
When the first basis-function-type in dFunction is set to
BF_NodeX_D1 for component X, BF_NodeY_D1 for component Y
and BF_NodeZ_D1 for component Z, then D1 applied to a
vector [u_x, u_y, u_z] gives:
[du_x/dx, du_y/dy, du_z/dz]
Note that in this case specifying explicitely dFunction is not
necessary, as BF_NodeX_D1, BF_NodeY_D1 and
BF_NodeZ_D1 are assigned by default as the “D1
derivatives” of BF_NodeX, BF_NodeY and BF_NodeZ.
This also holds for BF_GroupOfNodes_X, BF_GroupOfNodes_Y
and BF_GroupOfNodes_Z.
When the first basis-function-type in dFunction is set to
BF_NodeX_D12 for component X and BF_NodeY_D12 for
component Y, then D1 applied to a vector [u_x, u_y] gives:
[du_x/dx, du_y/dy, du_y/dx + du_x/dy]
D2
Applies the operator specified in the second argument of dFunction
{ basis-function-type, basis-function-type }
(see FunctionSpace). This is currently only used for
nodal-interpolated vector fields (interpolated with BF_Node_X,
BF_Node_Y, BF_Node_Z)
More specifically, when the second basis-function-type is to
BF_NodeX_D2 for component X, BF_NodeY_D2 for component Y
and BF_NodeZ_D2 for component Z, then D2 applied to a
vector [u_x, u_y, u_z] gives:
[du_y/dx + du_x/dy, du_z/dy + du_y/dz, du_x/dz + du_z/dx]
Note that in this case specifying explicitely dFunction is not
necessary, as BF_NodeX_D2, BF_NodeY_D2 and
BF_NodeZ_D2 are assigned by default as the “D2
derivatives” of BF_NodeX, BF_NodeY and BF_NodeZ.
This also holds for BF_GroupOfNodes_X, BF_GroupOfNodes_Y
and BF_GroupOfNodes_Z.
Notes:
Grad, Curl and Div can be applied
to 0, 1 and 2-forms respectively, the exterior derivative operator d
is usually preferred with such fields.
Previous: Fields, Up: Expressions [Contents][Index]
Macros are defined as follows:
Macro string | expression-char
Begins the declaration of a user-defined file macro named
string. The body of the macro starts on the line after
‘Macro string’, and can contain any GetDP command.
Return
Ends the body of the current user-defined file macro. Macro declarations cannot be imbricated, and must be made outside any GetDP object.
Macro ( expression-char , expression-char ) ;
Begins the declaration of a user-defined string macro. The body of the macro is given explicitly as the second argument.
Macros, loops and conditionals can be used in any of the following objects: Group, Function, Constraint (as well as in a contraint-case), FunctionSpace, Formulation (as well as in the quantity and equation defintions), Resolution (as well as resolution-term, system defintion and operations), PostProcessing (in the definition of the PostQuantities) and PostOperation (as well as in the operation list).
loop:
Call string | expression-char;
Executes the body of a (previously defined) macro named string.
For ( expression-cst : expression-cst )
Iterates from the value of the first expression-cst to the value of
the second expression-cst, with a unit incrementation step. At each
iteration, the commands comprised between ‘For ( expression-cst
: expression-cst )’ and the matching EndFor are executed.
For ( expression-cst : expression-cst : expression-cst )
Iterates from the value of the first expression-cst to the value of the
second expression-cst, with a positive or negative incrementation step
equal to the third expression-cst. At each iteration, the commands
comprised between ‘For ( expression-cst : expression-cst :
expression-cst )’ and the matching EndFor are executed.
For string In { expression-cst : expression-cst }
Iterates from the value of the first expression-cst to the value of the
second expression-cst, with a unit incrementation step. At each iteration,
the value of the iterate is affected to an expression named string,
and the commands comprised between ‘For string In {
expression-cst : expression-cst }’ and the matching EndFor are
executed.
For string In { expression-cst : expression-cst : expression-cst }
Iterates from the value of the first expression-cst to the value of the
second expression-cst, with a positive or negative incrementation step
equal to the third expression-cst. At each iteration, the value of the
iterate is affected to an expression named string, and the commands
comprised between ‘For string In { expression-cst :
expression-cst : expression-cst }’ and the matching EndFor are
executed.
EndFor
Ends a matching For command.
If ( expression-cst )
The body enclosed between ‘If ( expression-cst )’ and the matching
ElseIf, Else or EndIf, is evaluated if expression-cst
is non-zero.
ElseIf ( expression-cst )
The body enclosed between ‘ElseIf ( expression-cst )’ and the next
matching ElseIf, Else or EndIf, is evaluated if
expression-cst is non-zero and none of the expression-cst of the
previous matching codes If and ElseIf were non-zero.
Else
The body enclosed between Else and the matching EndIf is evaluated
if none of the expression-cst of the previous matching codes
If and ElseIf were non-zero.
EndIf
Ends a matching If command.
LevelTest
Variable equal to the level of imbrication of a body in an
If-EndIf test.
Parse [ expression-char ];
Parse the given string.
Next: Types for objects, Previous: Expressions, Up: Top [Contents][Index]
This chapter presents the formal definition of the ten GetDP objects mentioned in Overview. To be concise, all the possible parameters for these objects are not given here (cf. the etc syntactic rule defined in Syntactic rules). Please refer to Types for objects, for the list of all available options.
| • Group | ||
| • Function | ||
| • Constraint | ||
| • FunctionSpace | ||
| • Jacobian | ||
| • Integration | ||
| • Formulation | ||
| • Resolution | ||
| • PostProcessing | ||
| • PostOperation |
Group: defining topological entitiesMeshes (grids) constitute the input data of GetDP. All that is needed by GetDP as a mesh is a file containing a list of nodes (with their coordinates) and a list of geometrical elements with, for each one, a number characterizing its geometrical type (i.e., line, triangle, quadrangle, tetrahedron, hexahedron, prism, etc.), a number characterizing the physical region to which it belongs and the list of its nodes. This minimal input set should be easy to extract from most of the classical mesh file formats (see Input file format, for a complete description of the mesh file format read by GetDP).
Groups of geometrical entities of various types can be considered and are used in many objects. There are region groups, of which the entities are regions, and function groups, with nodes, edges, facets, volumes, groups of nodes, edges of tree, facets of tree, … of regions.
Amongst region groups, elementary and global groups can be distinguished: elementary groups are relative to single regions (e.g., physical regions in which piecewise defined functions or constraints can be defined) while global groups are relative to sets of regions for which given treatments have to be performed (e.g., domain of integration, support of a function space, etc.).
Groups of function type contain lists of entities built on some region groups (e.g., nodes for nodal elements, edges for edge elements, edges of tree for gauge conditions, groups of nodes for floating potentials, elements on one side of a surface for cuts, etc.).
A definition of initially empty groups can be obtained thanks to a
DefineGroup command, so that their identifiers exist and can be
referred to in other objects, even if these groups are not explicitly
defined. This procedure is similar to the DefineConstant procedure
introduced for constants in Constants.
The syntax for the definition of groups is:
Group {
< DefineGroup [ group-id <{integer}> <,…> ]; > …
< group-id = group-def; > …
< group-id += group-def; > …
< group-id -= group-def; > …
< affectation > …
< loop > …
}
with
group-id:
string |
string ~ { expression-cst }
group-def:
group-type [ group-list <, group-sub-type group-list > ] |
group-id <{<integer>}> |
#group-list
group-type:
Region | Global | NodesOf | EdgesOf | etc
group-list:
All | group-list-item | { group-list-item <,…> }
group-list-item:
integer |
integer : integer |
integer : integer : integer |
group-id <{<integer>}>
group-sub-type:
Not | StartingOn | OnPositiveSideOf | etc
Notes:
i:j replaces the list of consecutive integers i,
i+1, …, j-1, j.
DefineGroup[group-id{n}] defines
the empty groups group-id{i}, i=1, …, n.
Such a definition is optional, i.e., each
group-id{i} can be separately defined, in any order.
#group-list is an abbreviation of Region[group-list].
See Types for Group, for the complete list of options and Group examples, for some examples.
Next: Constraint, Previous: Group, Up: Objects [Contents][Index]
Function: defining global and piecewise expressionsA user-defined function can be global in space or piecewise defined in region groups. A physical characteristic is an example of a piecewise defined function (e.g., magnetic permeability, electric conductivity, etc.) and can be simply a constant, for linear materials, or a function of one or several arguments for nonlinear materials. Such functions can of course depend on space coordinates or time, which can be needed to express complex constraints.
A definition of initially empty functions can be made thanks to the
DefineFunction command so that their identifiers exist and can be
referred to (but cannot be used) in other objects. The syntax for the
definition of functions is:
Function {
< DefineFunction [ function-id <,…> ]; > …
< function-id [ < group-def <, group-def > > ] = expression; > …
< affectation > …
< loop > …
}
with
function-id: string
Note:
Region type, and
indicates on which region the (piecewise) function is defined.
The second optional group-def in brackets, also of Region type, defines
an association with a second region for mutual contributions.
A default piecewise function can be defined with All for group-def,
for all the other non-defined regions.
Warning: it is incorrect to write f[reg1]=1; g[reg2]=f[]+1; since the
domains of definition of f[] and g[] don’t match.
***.
See Types for Function, for the complete list of built-in functions and Function examples, for some examples.
Next: FunctionSpace, Previous: Function, Up: Objects [Contents][Index]
Constraint: specifying constraints on function spaces and formulationsConstraints can be referred to in FunctionSpace objects to be
used for boundary conditions, to impose global quantities or to
initialize quantities. These constraints can be expressed with
functions or be imposed by the pre-resolution of another discrete
problem. Other constraints can also be defined, e.g., constraints of
network type for the definition of circuit connections, to be used in
Formulation objects.
The syntax for the definition of constraints is:
Constraint {
{ < Append < expression-cst >; >
Name constraint-id; Type constraint-type;
Case {
{ Region group-def; < Type constraint-type; >
< SubRegion group-def; > < TimeFunction expression; >
< RegionRef group-def; > < SubRegionRef group-def; >
< Coefficient expression; > < Function expression; >
< Filter expression; >
constraint-val; } …
< loop > …
}
| Case constraint-case-id {
{ Region group-def; < Type constraint-type; >
constraint-case-val; } …
< loop > …
} …
} …
< affectation > …
< loop > …
}
with
constraint-id:
constraint-case-id:
string |
string ~ { expression-cst }
constraint-type:
Assign | Init | Network | Link | etc
constraint-val:
Value expression | NameOfResolution resolution-id | etc
constraint-case-val:
Branch { integer, integer } | etc
Notes:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
Constraint of the same Name with additional Cases.
Case
fields is applied to all the cases of the constraint, unless other types are
explicitly given in these cases. The default type is Assign.
Region group-def will be the main
group-list argument of the group-def to be built for the
constraints of FunctionSpaces. The optional region type
SubRegion group-def will be the argument of the associated
group-sub-type.
Value of constraint-val cannot be time
dependent ($Time) because it is evaluated only once during the
pre-processing (for efficiency reasons). Time dependences must be defined
in TimeFunction expression.
See Types for Constraint, for the complete list of options and Constraint examples, for some examples.
Next: Jacobian, Previous: Constraint, Up: Objects [Contents][Index]
FunctionSpace: building function spacesA FunctionSpace is characterized by the type of its interpolated
fields, one or several basis functions and optional constraints (in
space and time). Subspaces of a function space can be defined (e.g.,
for the use with hierarchical elements), as well as direct associations of
global quantities (e.g., floating potential, electric charge, current,
voltage, magnetomotive force, etc.).
A key point is that basis functions are defined by any number of subsets of functions, being added. Each subset is characterized by associated built-in functions for evaluation, a support of definition and a set of associated supporting geometrical entities (e.g., nodes, edges, facets, volumes, groups of nodes, edges incident to a node, etc.). The freedom in defining various kinds of basis functions associated with different geometrical entities to interpolate a field permits to build made-to-measure function spaces adapted to a wide variety of field approximations (see FunctionSpace examples).
The syntax for the definition of function spaces is:
FunctionSpace {
{ < Append < expression-cst >; >
Name function-space-id;
Type function-space-type;
BasisFunction {
{ Name basis-function-id; NameOfCoef coef-id;
Function basis-function-type
< { Quantity quantity-id;
Formulation formulation-id { expression-cst };
Group group-def;
Resolution resolution-id { expression-cst } } >;
< dFunction { basis-function-type, basis-function-type } ; >
Support group-def; Entity group-def; } …
}
< SubSpace {
{ < Append < expression-cst >; >
Name sub-space-id;
NameOfBasisFunction basis-function-list; } …
} >
< GlobalQuantity {
{ Name global-quantity-id; Type global-quantity-type;
NameOfCoef coef-id; } …
} >
< Constraint {
{ NameOfCoef coef-id;
EntityType Auto | group-type; < EntitySubType group-sub-type; >
NameOfConstraint constraint-id <{}>; } …
} >
} …
< affectation > …
< loop > …
}
with
function-space-id:
formulation-id:
resolution-id:
string |
string ~ { expression-cst }
basis-function-id:
coef-id:
sub-space-id:
global-quantity-id:
string
function-space-type:
Scalar | Vector | Form0 | Form1 | etc
basis-function-type:
BF_Node | BF_Edge | etc
basis-function-list:
basis-function-id | { basis-function-id <,…> }
global-quantity-type:
AliasOf | AssociatedWith
Notes:
Append < expression-cst > (when the optional level
expression-cst is strictly positive; its omission fixes it to a top
value) permits to append an existing
FunctionSpace of the same Name with additional
BasisFunctions, SubSpaces, GlobalQuantity’s and
Constraints,
or an existing SubSpace of the same Name with additional
NameOfBasisFunction’s. If the Append FunctionSpace level is 2,
the Append SubSpace level is automatically 1 if omitted.
Entity of
a BasisFunction is the same as that of the associated Support,
it is replaced by All for more efficient treatments during the
computation process (this prevents the construction and the analysis of a list
of geometrical entities).
Name for several BasisFunction fields permits to
define piecewise basis functions; separate NameOfCoefs must be
defined for those fields.
Group of type group-type
(Auto automatically fixes it as the Entity group-def
type of the related BasisFunction), using the
Region defined in a Constraint object as its main
argument, and the optional SubRegion in the same object as a
group-sub-type argument.
BF_Global or BF_dGlobal) needs
parameters, i.e., it is given by the quantity (quantity-id)
pre-computed from multiresolutions performed on multiformulations.
dFunction { basis-function-type , basis-function-type
}. These derivates can be accessed using the special D1 and
D2 operators (see Fields).
See Types for FunctionSpace, for the complete list of options and FunctionSpace examples, for some examples.
Next: Integration, Previous: FunctionSpace, Up: Objects [Contents][Index]
Jacobian: defining jacobian methodsJacobian methods can be referred to in Formulation and
PostProcessing objects to be used in the computation of integral
terms and for changes of coordinates. They are based on Group
objects and define the geometrical transformations applied to the
reference elements (i.e., lines, triangles, quadrangles, tetrahedra,
prisms, hexahedra, etc.). Besides the classical lineic, surfacic and
volume Jacobians, the Jacobian object allows the construction of
various transformation methods (e.g., infinite transformations for
unbounded domains) thanks to dedicated jacobian methods.
The syntax for the definition of Jacobian methods is:
Jacobian {
{ < Append < expression-cst >; >
Name jacobian-id;
Case {
{ Region group-def | All;
Jacobian jacobian-type < { expression-cst-list } >; } …
}
} …
}
with
jacobian-id: string jacobian-type: Vol | Sur | VolAxi | etc
Note:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
Jacobian of the same Name with additional Cases.
Jacobian object is defined by Region All
and must follow all the other cases.
See Types for Jacobian, for the complete list of options and Jacobian examples, for some examples.
Next: Formulation, Previous: Jacobian, Up: Objects [Contents][Index]
Integration: defining integration methodsVarious numerical or analytical integration methods can be referred to in
Formulation and PostProcessing objects to be used in the
computation of integral terms, each with a set of particular options (number of
integration points for quadrature methods—which can be linked to an error
criterion for adaptative methods, definition of transformations for singular
integrations, etc.). Moreover, a choice can be made between several
integration methods according to a criterion (e.g., on the proximity between
the source and computation points in integral formulations).
The syntax for the definition of integration methods is:
Integration {
{ < Append < expression-cst >; >
Name integration-id; < Criterion expression; >
Case {
< { Type integration-type;
Case {
{ GeoElement element-type; NumberOfPoints expression-cst } …
}
} … >
< { Type Analytic; } … >
}
} …
}
with
integration-id: string integration-type: Gauss | etc element-type: Line | Triangle | Tetrahedron etc
Note:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
Integration of the same Name with additional Cases.
See Types for Integration, for the complete list of options and Integration examples, for some examples.
Next: Resolution, Previous: Integration, Up: Objects [Contents][Index]
Formulation: building equationsThe Formulation tool permits to deal with volume, surface and
line integrals with many kinds of densities to integrate, written in a
form that is similar to their symbolic expressions (it uses the same
expression syntax as elsewhere in GetDP), which therefore permits
to directly take into account various kinds of elementary matrices
(e.g., with scalar or cross products, anisotropies, nonlinearities, time
derivatives, various test functions, etc.). In case nonlinear physical
characteristics are considered, arguments are used for associated
functions. In that way, many formulations can be directly written in the
data file, as they are written symbolically. Fields involved in each
formulation are declared as belonging to beforehand defined function
spaces. The uncoupling between formulations and function spaces allows
to maintain a generality in both their definitions.
A Formulation is characterized by its type, the involved
quantities (of local, global or integral type) and a list of equation
terms. Global equations can also be considered, e.g., for the coupling
with network relations.
The syntax for the definition of formulations is:
Formulation {
{ < Append < expression-cst >; >
Name formulation-id; Type formulation-type;
Quantity {
{ Name quantity-id; Type quantity-type;
NameOfSpace function-space-id <{}>
< [ sub-space-id | global-quantity-id ] >;
< Symmetry expression-cst; >
< [ expression ]; In group-def;
Jacobian jacobian-id; Integration integration-id; >
< IndexOfSystem integer; > } …
}
Equation {
< local-term-type
{ < term-op-type > [ expression, expression ];
In group-def; Jacobian jacobian-id;
Integration integration-id; } > …
< GlobalTerm
{ < term-op-type > [ expression, expression ];
In group-def; < SubType equation-term-sub-type; > } > …
< GlobalEquation
{ Type Network; NameOfConstraint constraint-id;
{ Node expression; Loop expression; Equation expression;
In group-def; } …
} > …
< affectation > …
< loop > …
}
} …
< affectation > …
< loop > …
}
with
formulation-id:
string |
string ~ { expression-cst }
formulation-type:
FemEquation | etc
local-term-type:
Integral | deRham
equation-term-sub-type:
Self (default) | Mutual | SelfAndMutual
quantity-type:
Local | Global | Integral
term-op-type:
DtDof | DtDtDof | Eig | JacNL | etc
Note:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
Formulation of the same Name with additional
Quantity’s and Equations.
IndexOfSystem permits to resolve ambiguous cases when several
quantities belong to the same function space, but to different systems of
equations. The integer parameter then specifies the index in the list
of an OriginSystem command (see Resolution).
GlobalTerm defines a term to be assembled in an equation associated
with a global quantity. This equation is a finite element equation if that
global quantity is linked with local quantities. The optional associated
SubType defines either self (default) or mutual contributions, or both.
Mutual contributions need piecewise functions defined on pairs or regions.
GlobalEquation defines a global equation to be assembled in the
matrix of the system.
See Types for Formulation, for the complete list of options and Formulation examples, for some examples.
Next: PostProcessing, Previous: Formulation, Up: Objects [Contents][Index]
Resolution: solving systems of equationsThe operations available in a Resolution include: the generation of a
linear system, its solving with various kinds of linear solvers, the saving
of the solution or its transfer to another system, the definition of various
time stepping methods, the construction of iterative loops for nonlinear
problems (Newton-Raphson and fixed point methods), etc. Multi-harmonic
resolutions, coupled problems (e.g., magneto-thermal) or linked problems
(e.g., pre-computations of source fields) are thus easily defined in GetDP.
The Resolution object is characterized by a list of systems to
build and their associated formulations, using time or frequency domain,
and a list of elementary operations:
Resolution {
{ < Append < expression-cst >; >
Name resolution-id; < Hidden expression-cst; >
System {
{ Name system-id; NameOfFormulation formulation-list;
< Type system-type; >
< Frequency expression-cst-list-item |
Frequency { expression-cst-list }; >
< DestinationSystem system-id; >
< OriginSystem system-id; | OriginSystem { system-id <,…> }; >
< NameOfMesh expression-char > < Solver expression-char >
< loop > } …
< loop > …
}
Operation {
< resolution-op; > …
< loop > …
}
} …
< affectation > …
< loop > …
}
with
resolution-id:
system-id:
string |
string ~ { expression-cst }
formulation-list:
formulation-id <{}> | { formulation-id <{}> <,…> }
system-type:
Real | Complex
resolution-op:
Generate[system-id] | Solve[system-id] | etc
Notes:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
Resolution of the same Name with additional
Systems and Operations.
Real. A frequency
domain analysis is defined through the definition of one or several
frequencies (Frequency expression-cst-list-item | Frequency {
expression-cst-list }). Complex systems of equations with no
predefined list of frequencies (e.g., in modal analyses) can be explicitely
defined with Type Complex.
NameOfMesh permits to explicitely specify the mesh to be used for the
construction of the system of equations.
Solver permits to explicitely specify the name of the solver
parameter file to use for the solving of the system of equations. This is
ony valid if GetDP was compiled against the default solver library (it is
the case if you downloaded a pre-compiled copy of GetDP from the internet).
DestinationSystem permits to specify the destination system of a
TransferSolution operation (see Types for Resolution).
OriginSystem permits to specify the systems from which ambiguous
quantity definitions can be solved (see Formulation).
See Types for Resolution, for the complete list of options and Resolution examples, for some examples.
Next: PostOperation, Previous: Resolution, Up: Objects [Contents][Index]
PostProcessing: exploiting computational resultsThe PostProcessing object is based on the quantities defined in a
Formulation and permits the construction (thanks to the
expression syntax) of any useful piecewise defined quantity of
interest:
PostProcessing {
{ < Append < expression-cst >; >
Name post-processing-id;
NameOfFormulation formulation-id <{}>; < NameOfSystem system-id; >
Quantity {
{ < Append < expression-cst >; >
Name post-quantity-id; Value { post-value … } } …
< loop > …
}
} …
< affectation > …
< loop > …
}
with
post-processing-id:
post-quantity-id:
string |
string ~ { expression-cst }
post-value:
Local { local-value } | Integral { integral-value }
local-value:
[ expression ]; In group-def; Jacobian jacobian-id;
integral-value:
[ expression ]; In group-def;
Integration integration-id; Jacobian jacobian-id;
Notes:
Append < expression-cst > (when the optional level
expression-cst is strictly positive; its omission fixes it to a top
value) permits to append an existing
PostProcessing of the same Name with additional
Values,
or an existing Quantity of the same Name with additional
Quantity’s. If the Append PostProcessing level is 2,
the Append Quantity level is automatically 1 if omitted.
Fixing the Append Quantity level to -n suppresses the
n lastly defined Quantity’s before appending.
PostOperation with the post-quantity-id[group-def]
command (see PostOperation).
NameOfSystem system-id is not given, the system is
automatically selected as the one to which the first quantity listed in
the Quantity field of formulation-id is associated.
See Types for PostProcessing, for the complete list of options and PostProcessing examples, for some examples.
Previous: PostProcessing, Up: Objects [Contents][Index]
PostOperation: exporting resultsThe PostOperation is the bridge between results obtained with GetDP
and the external world. It defines several elementary operations on
PostProcessing quantities (e.g., plot on a region, section on a
user-defined plane, etc.), and outputs the results in several file formats.
PostOperation {
{ < Append < expression-cst >; >
Name post-operation-id; NameOfPostProcessing post-processing-id;
< Hidden expression-cst; >
< Format post-operation-fmt; >
< TimeValue expression-cst-list; > < TimeImagValue expression-cst-list; >
< LastTimeStepOnly < expression-cst >; >
< OverrideTimeStepValue expression-cst; >
< NoMesh expression-cst; > < AppendToExistingFile expression-cst; >
< ResampleTime[expression-cst, expression-cst, expression-cst]; >
< AppendTimeStepToFileName < expression-cst >; >
Operation {
< post-operation-op; > …
}
} …
< affectation > …
< loop > …
} |
PostOperation < (Append < expression-cst >) > post-operation-id UsingPost post-processing-id {
< post-operation-op; > …
} …
with
post-operation-id:
string |
string ~ { expression-cst }
post-operation-op:
Print[ post-quantity-id <[group-def]>, print-support <,print-option> … ] |
Print[ expression-list, Format "string" <,print-option> … ] |
PrintGroup[ group-id, print-support <,print-option> … ] |
Echo[ "string" <,print-option> … ] |
CreateDir [ "string" ] |
DeleteFile [ "string" ] |
SendMergeFileRequest[ expression-char ] |
< loop > …
etc
print-support:
OnElementsOf group-def | OnRegion group-def | OnGlobal | etc
print-option:
File expression-char | Format post-operation-fmt | etc
post-operation-fmt:
Table | TimeTable | etc
Notes:
Append < expression-cst > (when the optional level
expression-cst is strictly positive) permits to append an existing
PostOperation of the same Name with additional
Operations.
PostOperation syntaxes are equivalent. The first one conforms to
the overall interface, but the second one is more concise.
Operation
field is applied to all the post-processing operations, unless other formats
are explicitly given in these operations with the Format option
(see Types for PostOperation). The default format is Gmsh.
ResampleTime option allows equidistant resampling of the time steps by a
spline interpolation. The parameters are: start time, stop time, time step.
[group-def] of the post-quantity-id
can only be used when this quantity has been defined as an
integral-value (see PostProcessing). In this case, the sum of all
elementary integrals is performed over the region group-def.
See Types for PostOperation, for the complete list of options and PostOperation examples, for some examples.
Next: Short examples, Previous: Objects, Up: Top [Contents][Index]
This chapter presents the complete list of choices associated with metasyntactic variables introduced for the ten GetDP objects.
Next: Types for Function, Previous: Types for objects, Up: Types for objects [Contents][Index]
GroupTypes in
group-type [ R1 <, group-sub-type R2 <, group-sub-type-2 R3 > > ]
group-type < group-sub-type < group-sub-type-2 > >:
Region
Regions in R1.
Global
Regions in R1
(variant of Region used with global BasisFunctions
BF_Global and BF_dGlobal).
NodesOf
Nodes of elements of R1
< Not: but not those of R2 >.
EdgesOf
Edges of elements of R1
< Not: but not those of R2 >.
FacetsOf
Facets of elements of R1
< Not: but not those of R2 >.
VolumesOf
Volumes of elements of R1
< Not: but not those of R2 >.
ElementsOf
Elements of regions in R1
< OnOneSideOf: only elements on one side
of R2 (non-automatic, i.e., both sides if both in R1) > |
< OnPositiveSideOf: only elements on positive (normal) side of R2
< , Not: but not those touching only its skin R3
(mandatory for free skins for correct separation of side layers) > >.
GroupsOfNodesOf
Groups of nodes of elements of R1 (a group is associated with each region).
GroupsOfEdgesOf
Groups of edges of elements of R1 (a group is associated with each region).
< InSupport: in a support R2 being a group of type ElementOf,
i.e., containing elements >.
GroupsOfEdgesOnNodesOf
Groups of edges incident to nodes of elements of R1 (a group is associated with each node).
< Not: but not those of R2) >.
GroupOfRegionsOf
Single group of elements of regions in R1 (with basis function BF_Region just one DOF is created for all elements of R1).
EdgesOfTreeIn
Edges of a tree of edges of R1
< StartingOn: a complete tree is first built on R2 >.
FacetsOfTreeIn
Facets of a tree of facets of R1
< StartingOn: a complete tree is first built on R2 >.
DualNodesOf
Dual nodes of elements of R1.
DualEdgesOf
Dual edges of elements of R1.
DualFacetsOf
Dual facets of elements of R1.
DualVolumesOf
Dual volumes of elements of R1.
Next: Types for Constraint, Previous: Types for Group, Up: Types for objects [Contents][Index]
Function| • Math functions | ||
| • Extended math functions | ||
| • Green functions | ||
| • Type manipulation functions | ||
| • Coordinate functions | ||
| • Miscellaneous functions |
Next: Extended math functions, Previous: Types for Function, Up: Types for Function [Contents][Index]
The following functions are the equivalent of the functions of the C or C++ math library. Unless indicated otherwise, arguments to these functions can be real or complex valued when used in expressions. When used in constant expressions (expression-cst, see Constants), only real-valued arguments are accepted.
math-function-id:
Exp
[expression]
Exponential function: e^expression.
Log
[expression]
Natural logarithm: ln(expression), expression>0.
Log10
[expression]
Base 10 logarithm: log10(expression), expression>0.
Sqrt
[expression]
Square root, expression>=0.
Sin
[expression]
Sine of expression.
Asin
[expression]
Arc sine (inverse sine) of expression in [-Pi/2,Pi/2], expression in [-1,1] (real valued only).
Cos
[expression]
Cosine of expression.
Acos
[expression]
Arc cosine (inverse cosine) of expression in [0,Pi], expression in [-1,1] (real valued only).
Tan
[expression]
Tangent of expression.
Atan
[expression]
Arc tangent (inverse tangent) of expression in [-Pi/2,Pi/2] (real valued only).
Atan2
[expression,expression]
Arc tangent (inverse tangent) of the first expression divided by the second, in [-Pi,Pi] (real valued only).
Sinh
[expression]
Hyperbolic sine of expression.
Cosh
[expression]
Hyperbolic cosine of expression.
Tanh
[expression]
Hyperbolic tangent of the real valued expression.
TanhC2
[expression]
Hyperbolic tangent of a complex valued expression.
Fabs
[expression]
Absolute value of expression (real valued only).
Abs
[expression]
Absolute value of expression.
Floor
[expression]
Rounds downwards to the nearest integer that is not greater than expression (real valued only).
Ceil
[expression]
Rounds upwards to the nearest integer that is not less than expression (real valued only).
Fmod
[expression,expression]
Remainder of the division of the first expression by the second, with the sign of the first (real valued only).
Min
[expression,expression]
Minimum of the two (scalar) expressions (real valued only).
Max
[expression,expression]
Maximum of the two (scalar) expressions (real valued only).
Sign
[expression]
-1 for expression less than zero and 1 otherwise (real valued only).
Jn
[expression]
Returns the Bessel function of the first kind of order given by the first expression for the value of the second expression (real valued only).
dJn
[expression]
Returns the derivative of the Bessel function of the first kind of order given by the first expression for the value of the second expression (real valued only).
Yn
[expression]
Returns the Bessel function of the second kind of order given by the first expression for the value of the second expression (real valued only).
dYn
[expression]
Returns the derivative of the Bessel function of the second kind of order given by the first expression for the value of the second expression (real valued only).
Next: Green functions, Previous: Math functions, Up: Types for Function [Contents][Index]
extended-math-function-id:
Cross
[expression,expression]
Cross product of the two arguments; expression must be a vector.
Hypot
[expression,expression]
Square root of the sum of the squares of its arguments.
Norm
[expression]
Absolute value if expression is a scalar; euclidian norm if expression is a vector.
SquNorm
[expression]
Square norm: Norm[expression]^2.
Unit
[expression]
Normalization: expression/Norm[expression]. Returns 0 if the norm is
smaller than 1.e-30.
Transpose
[expression]
Transposition; expression must be a tensor.
Inv
[expression]
Inverse of the tensor expression.
Det
[expression]
Determinant of the tensor expression.
Rotate
[expression,expression,expression,expression]
Rotation of a vector or tensor given by the first expression by the angles in radians given by the last three expression values around the x-, y- and z-axis.
TTrace
[expression]
Trace; expression must be a tensor.
Cos_wt_p
[]{expression-cst,expression-cst}
The first parameter represents the angular frequency and the second
represents the phase. If the type of the current system is Real,
F_Cos_wt_p[]{w,p} is identical to Cos[w*$Time+p]. If the
type of the current system is Complex, it is identical to
Complex[Cos[p],Sin[p]].
Sin_wt_p
[]{expression-cst,expression-cst}
The first parameter represents the angular frequency and the second
represents the phase. If the type of the current system is Real,
F_Sin_wt_p[]{w,p} is identical to Sin[w*$Time+p]. If the
type of the current system is Complex, it is identical to
Complex[Sin[p],-Cos[p]].
Period
[expression]{expression-cst}
Fmod[expression,expression-cst]
+
(expression<0 ? expression-cst : 0);
the result is always in [0,expression-cst[.
Interval
[expression,expression,expression]{expression-cst,
expression-cst,expression-cst}
Not documented yet.
Next: Type manipulation functions, Previous: Extended math functions, Up: Types for Function [Contents][Index]
The Green functions are only used in integral quantities (see Formulation). The first parameter represents the dimension of the problem:
1D:
r = Fabs[$X-$XS]
2D:
r = Sqrt[($X-$XS)^2+($Y-$YS)^2]
3D:
r = Sqrt[($X-$XS)^2+($Y-$YS)^2+($Z-$ZS)^2]
The triplets of values given in the definitions below correspond to the
1D, 2D and 3D cases.
green-function-id:
Laplace
[]{expression-cst}
r/2, 1/(2*Pi)*ln(1/r), 1/(4*Pi*r).
GradLaplace
[]{expression-cst}
Gradient of Laplace relative to the destination point ($X,
$Y, $Z).
Helmholtz
[]{expression-cst, expression-cst}
exp(j*k0*r)/(4*Pi*r), where k0 is given by the second parameter.
GradHelmholtz
[]{expression-cst, expression-cst}
Gradient of Helmholtz relative to the destination point ($X,
$Y, $Z).
Next: Coordinate functions, Previous: Green functions, Up: Types for Function [Contents][Index]
type-function-id:
Complex
[expression-list]
Creates a (multi-harmonic) complex expression from an number of real-valued expressions. The number of expressions in expression-list must be even.
Complex_MH
[expression-list]{expression-cst-list}
Not documented yet.
Re
[expression]
Takes the real part of a complex-valued expression.
Im
[expression]
Takes the imaginary part of a complex-valued expression.
Conj
[expression]
Computes the conjugate of a complex-valued expression.
Cart2Pol
[expression]
Converts the cartesian form (reale, imaginary) of a complex-valued expression into polar form (amplitude, phase [radians]).
Vector
[expression,expression,expression]
Creates a vector from 3 scalars.
Tensor
[expression,expression,expression,expression,expression,expression,
expression,expression,expression]
Creates a second-rank tensor of order 3 from 9 scalars, by row:
[ scalar0 scalar1 scalar2 ] [ CompXX CompXY CompXZ ]
T = [ scalar3 scalar4 scalar5 ] = [ CompYX CompYY CompYZ ]
[ scalar6 scalar7 scalar8 ] [ CompZX CompZY CompZZ ]
TensorV
[expression,expression,expression]
Creates a second-rank tensor of order 3 from 3 row vectors:
[ vector0 ]
T = [ vector1 ]
[ vector2 ]
TensorSym
[expression,expression,expression,expression,expression,expression]
Creates a symmetrical second-rank tensor of order 3 from 6 scalars.
TensorDiag
[expression,expression,expression]
Creates a diagonal second-rank tensor of order 3 from 3 scalars.
SquDyadicProduct
[expression]
Dyadic product of the vector given by expression with itself.
CompX
[expression]
Gets the X component of a vector.
CompY
[expression]
Gets the Y component of a vector.
CompZ
[expression]
Gets the Z component of a vector.
CompXX
[expression]
Gets the XX component of a tensor.
CompXY
[expression]
Gets the XY component of a tensor.
CompXZ
[expression]
Gets the XZ component of a tensor.
CompYX
[expression]
Gets the YX component of a tensor.
CompYY
[expression]
Gets the YY component of a tensor.
CompYZ
[expression]
Gets the YZ component of a tensor.
CompZX
[expression]
Gets the ZX component of a tensor.
CompZY
[expression]
Gets the ZY component of a tensor.
CompZZ
[expression]
Gets the ZZ component of a tensor.
Cart2Sph
[expression]
Gets the tensor for transformation of vector from cartesian to spherical coordinates.
Cart2Cyl
[expression]
Gets the tensor for transformation of vector from cartesian to cylindric coordinates. E.g. to convert a vector with (x,y,z)-components to one with (radial, tangential, axial)-components: Cart2Cyl[XYZ[]] * vector
UnitVectorX
[]
Creates a unit vector in x-direction.
UnitVectorY
[]
Creates a unit vector in y-direction.
UnitVectorZ
[]
Creates a unit vector in z-direction.
Next: Miscellaneous functions, Previous: Type manipulation functions, Up: Types for Function [Contents][Index]
coord-function-id:
X
[]
Gets the X coordinate.
Y
[]
Gets the Y coordinate.
Z
[]
Gets the Z coordinate.
XYZ
[]
Gets X, Y and Z in a vector.
Previous: Coordinate functions, Up: Types for Function [Contents][Index]
misc-function-id:
Printf
[expression]
Prints the value of expression when evaluated. (MPI_Printf
can be use instead, to print the message for all MPI ranks.)
Rand
[expression]
Returns a pseudo-random number in [0, expression].
Normal
[]
Computes the normal to the element.
NormalSource
[]
Computes the normal to the source element (only valid in a quantity of Integral type).
Tangent
[]
Computes the tangent to the element (only valid for line elements).
TangentSource
[]
Computes the tangent to the source element (only valid in a quantity of Integral type and only for line elements).
ElementVol
[]
Computes the element’s volume.
SurfaceArea
[]{expression-cst-list}
Computes the area of the physical surfaces in expression-cst-list or of the actual surface if expression-cst-list is empty.
GetVolume
[]
Computes the volume of the actual physical group.
CompElementNum
[]
Returns 0 if the current element and the current source element are identical.
GetNumElements
[]{expression-cst-list}
Counts the elements of physical numbers in expression-cst-list or of the actual region if expression-cst-list is empty.
ElementNum
[]
Returns the tag (number) of the current element.
QuadraturePointIndex
[]
Returns the index of the current quadrature point.
AtIndex
[expression]{expression-cst-list}
Returns the i-th entry of expression-cst-list. This can be used to get an element in a list, using an index that is computed at runtime.
InterpolationLinear
[expression]{expression-cst-list}
Linear interpolation of points. The number of constant expressions in expression-cst-list must be even.
dInterpolationLinear
[expression]{expression-cst-list}
Derivative of linear interpolation of points. The number of constant expressions in expression-cst-list must be even.
InterpolationBilinear
[expression,expression]{expression-cst-list}
Bilinear interpolation of a table based on two variables.
dInterpolationBilinear
[expression,expression]{expression-cst-list}
Derivative of bilinear interpolation of a table based on two variables. The result is a vector.
InterpolationAkima
[expression]{expression-cst-list}
Akima interpolation of points. The number of constant expressions in expression-cst-list must be even.
dInterpolationAkima
[expression]{expression-cst-list}
Derivative of Akima interpolation of points. The number of constant expressions in expression-cst-list must be even.
Order
[quantity]
Returns the interpolation order of the quantity.
Field
[expression]
Evaluate the last one of the fields (“views”) loaded with
GmshRead (see Types for Resolution), at the point
expression. Common usage is thus Field[XYZ[]].
Field
[expression]{expression-cst-list}
Idem, but evaluate all the fields corresponding to the tags in the list, and sum all the values. A field having no value at the given position does not produce an error: its contribution to the sum is simply zero.
ScalarField
[expression]{expression-cst-list}
Idem, but consider only real-valued scalar fields. A second optional argument is the value of the time step. A third optional argument is a boolean flag to indicate that the interpolation should be performed (if possible) in the same element as the current element.
VectorField
[expression]{expression-cst-list}
Idem, but consider only real-valued vector fields. Optional arguments
are treated in the same way as for ScalarField.
TensorField
[expression]{expression-cst-list}
Idem, but consider only real-valued tensor fields. Optional arguments
are treated in the same way as for ScalarField.
ComplexScalarField
[expression]{expression-cst-list}
Idem, but consider only complex-valued scalar fields. Optional arguments
are treated in the same way as for ScalarField.
ComplexVectorField
[expression]{expression-cst-list}
Idem, but consider only complex-valued vector fields. Optional arguments
are treated in the same way as for ScalarField.
ComplexTensorField
[expression]{expression-cst-list}
Idem, but consider only complex-valued tensor fields. Optional arguments
are treated in the same way as for ScalarField.
Distance
[expression]{expression-cst}
Evaluate the distance between the point (whose x, y, z coordinates are given as a vector argument) and a vector valued view, interpreted as a displacement field (i.e. compute the minimal distance between the point and the deformed mesh in the view).
GetCpuTime
[]
Returns current CPU time, in seconds (total amount of time spent executing in user mode since GetDP was started).
GetWallClockTime
[]
Returns the current wall clock time, in seconds (total wall clock time since GetDP was started).
GetMemory
[]
Returns the current memory usage, in megabytes (maximum resident set size).
SetNumberRunTime
[expression]{char-expression}
Sets the char-expression ONELAB variable at run-time to expression.
SetNumberRunTimeWithChoices
[expression]{char-expression}
Same as SetNumberRunTime, but adds the value to the choices of
the ONELAB variable (i.e. in the same way as SendToServer in
PostOperation, which are used for plotting the history of the
variable).
GetNumberRunTime
[ <expression> ]{char-expression}
Gets the value of the char-expression ONELAB variable at run-time. If the optional expression is provided, it is used as a default value if ONELAB is not available.
SetVariable
[ expression <,…> ]{ $variable-id }
Sets the value of the runtime variable $variable-id to the
value of the first expression, and returns this value. If
optional expressions are provided, they are appended to the
variable name, separated by _.
GetVariable
[ <expression> <,…> ]{ $variable-id }
Gets the value of the runtime variable $variable-id. If
the optional expressions are provided, they are appended to the
variable name, separated by _.
ValueFromIndex
[ ]{ expression-cst-list }
Treats expression-cst-list as a map of (entity, value) pairs. Useful to specify nodal or element-wise constraints, where entity is the node (mesh vertex) or element number (tag).
VectorFromIndex
[ ]{ expression-cst-list }
Same ValueFromIndex, but with 3 scalar values per entity.
ValueFromTable
[ expression ]{ char-expression }
Accesses the map char-expression created by a NodeTable or
ElementTable PostOperation. If the map is not available
(e.g. in pre-processing), or if the entity is not found in the map, use
expression as default value. Useful to specify nodal or
element-wise constraints, where entity is the node (mesh vertex)
or element number (tag).
Next: Types for FunctionSpace, Previous: Types for Function, Up: Types for objects [Contents][Index]
Constraintconstraint-type:
Assign
To assign a value (e.g., for boundary condition).
Init
To give an initial value (e.g., initial value in a time domain
analysis). If two values are provided (with Value [
expression, expression ]), the first value can be used
using the InitSolution1 operation. This is mainly useful for the
Newmark time-stepping scheme.
AssignFromResolution
To assign a value to be computed by a pre-resolution.
InitFromResolution
To give an initial value to be computed by a pre-resolution.
Network
To describe the node connections of branches in a network.
Link
To define links between degrees of freedom in the constrained region with
degrees of freedom in a “reference” region, with some coefficient. For
example, to link the degrees of freedom in the contrained region Left
with the degrees of freedom in the reference region Right, located Pi
units to the right of the region Left along the X-axis, with the
coeficient -1, one could write:
{ Name periodic;
Case {
{ Region Left; Type Link ; RegionRef Right;
Coefficient -1; Function Vector[X[]+Pi, Y[], Z[]] ;
< FunctionRef XYZ[]; >
}
}
}
In this example, Function defines the mapping that translates the
geometrical elements in the region Left by Pi units along the
X-axis, so that they correspond with the elements in the reference
region Right. For this mapping to work, the meshes of Left
and Right must be identical. (The optional FunctionRef
function allows to transform the reference region, useful e.g. to avoid
generating overlapping meshes for rotational links.)
LinkCplx
To define complex-valued links between degrees of freedom. The syntax is the
same as for constraints of type Link, but Coeficient can be
complex.
Next: Types for Jacobian, Previous: Types for Constraint, Up: Types for objects [Contents][Index]
FunctionSpacefunction-space-type:
Form0
0-form, i.e., scalar field of potential type.
Form1
1-form, i.e., curl-conform field (associated with a curl).
Form2
2-form, i.e., div-conform field (associated with a divergence).
Form3
3-form, i.e., scalar field of density type.
Form1P
1-form perpendicular to the z=0 plane, i.e., perpendicular curl-conform field (associated with a curl).
Form2P
2-form in the z=0 plane, i.e., parallel div-conform field (associated with a divergence).
Scalar
Scalar field.
Vector
Vector field.
basis-function-type:
BF_Node
Nodal function (on NodesOf, value Form0).
BF_Edge
Edge function (on EdgesOf, value Form1).
BF_Facet
Facet function (on FacetsOf, value Form2).
BF_Volume
Volume function (on VolumesOf, value Form3).
BF_GradNode
Gradient of nodal function
(on NodesOf, value Form1).
BF_CurlEdge
Curl of edge function
(on EdgesOf, value Form2).
BF_DivFacet
Divergence of facet function
(on FacetsOf, value Form3).
BF_GroupOfNodes
Sum of nodal functions
(on GroupsOfNodesOf, value Form0).
BF_GradGroupOfNodes
Gradient of sum of nodal functions
(on GroupsOfNodesOf, value Form1).
BF_GroupOfEdges
Sum of edge functions
(on GroupsOfEdgesOf, value Form1).
BF_CurlGroupOfEdges
Curl of sum of edge functions
(on GroupsOfEdgesOf, value Form2).
BF_PerpendicularEdge
1-form (0, 0, BF_Node) (on NodesOf, value Form1P).
BF_CurlPerpendicularEdge
Curl of 1-form (0, 0, BF_Node) (on NodesOf, value Form2P).
BF_GroupOfPerpendicularEdge
Sum of 1-forms (0, 0, BF_Node) (on NodesOf, value Form1P).
BF_CurlGroupOfPerpendicularEdge
Curl of sum of 1-forms (0, 0, BF_Node) (on NodesOf,
value Form2P).
BF_PerpendicularFacet
2-form (90 degree rotation of BF_Edge)
(on EdgesOf, value Form2P).
BF_DivPerpendicularFacet
Div of 2-form (90 degree rotation of BF_Edge)
(on EdgesOf, value Form3).
BF_Region
Unit value 1 (on Region or GroupOfRegionsOf, value Scalar).
BF_RegionX
Unit vector (1, 0, 0) (on Region, value Vector).
BF_RegionY
Unit vector (0, 1, 0) (on Region, value Vector).
BF_RegionZ
Unit vector (0, 0, 1) (on Region, value Vector).
BF_Global
Global pre-computed quantity
(on Global, value depends on parameters).
BF_dGlobal
Exterior derivative of global pre-computed quantity
(on Global, value depends on parameters).
BF_NodeX
Vector (BF_Node, 0, 0)
(on NodesOf, value Vector).
BF_NodeY
Vector (0, BF_Node, 0)
(on NodesOf, value Vector).
BF_NodeZ
Vector (0, 0, BF_Node)
(on NodesOf, value Vector).
BF_Zero
Zero value 0 (on all regions, value Scalar).
BF_One
Unit value 1 (on all regions, value Scalar).
global-quantity-type:
AliasOf
Another name for a name of coefficient of basis function.
AssociatedWith
A global quantity associated with a name of coefficient of basis function, and therefore with this basis function.
Next: Types for Integration, Previous: Types for FunctionSpace, Up: Types for objects [Contents][Index]
Jacobianjacobian-type:
Vol
Volume Jacobian, for n-D regions in n-D geometries, n = 1, 2 or 3.
Sur
Surface Jacobian, for (n-1)-D regions in n-D geometries, n = 1, 2 or 3.
Lin
Line Jacobian, for (n-2)-D regions in n-D geometries, n = 2 or 3.
VolAxi
Axisymmetrical volume Jacobian (1st type: r), for 2-D regions in axisymmetrical geometries.
SurAxi
Axisymmetrical surface Jacobian (1st type: r), for 1-D regions in axisymmetrical geometries.
VolAxiSqu
Axisymmetrical volume Jacobian (2nd type: r^2), for 2-D regions in axisymmetrical geometries.
VolSphShell
Volume Jacobian with spherical shell transformation, for n-D regions in n-D geometries, n = 2 or 3.
Parameters: radius-internal, radius-external <, center-X, center-Y, center-Z, power, 1/infinity >.
VolCylShell
Volume Jacobian with cylindrical shell transformation, for n-D
regions in n-D geometries, n = 2 or 3. For n=2,
VolCylShell is identical to VolSphShell. For n=3,
the axis of the cylinder is supposed to be along the z axis.
Parameters: radius-internal, radius-external <, center-X, center-Y, center-Z, power, 1/infinity >.
VolAxiSphShell
Same as VolAxi, but with spherical shell transformation.
Parameters: radius-internal, radius-external <, center-X, center-Y, center-Z, power, 1/infinity >.
VolAxiSquSphShell
Same as VolAxiSqu, but with spherical shell transformation.
Parameters: radius-internal, radius-external <, center-X, center-Y, center-Z, power, 1/infinity >.
VolRectShell
Volume Jacobian with rectangular shell transformation, for n-D regions in n-D geometries, n = 2 or 3.
Parameters: radius-internal, radius-external <, direction, center-X, center-Y, center-Z, power, 1/infinity >.
VolAxiRectShell
Same as VolAxi, but with rectangular shell transformation.
Parameters: radius-internal, radius-external <, direction, center-X, center-Y, center-Z, power, 1/infinity >.
VolAxiSquRectShell
Same as VolAxiSqu, but with rectangular shell transformation.
Parameters: radius-internal, radius-external <, direction, center-X, center-Y, center-Z, power, 1/infinity >.
Next: Types for Formulation, Previous: Types for Jacobian, Up: Types for objects [Contents][Index]
Integrationintegration-type:
Gauss
Numerical Gauss integration.
GaussLegendre
Numerical Gauss integration obtained by application of a multiplicative rule on the one-dimensional Gauss integration.
element-type:
Line
Line (2 nodes, 1 edge, 1 volume) (#1).
Triangle
Triangle (3 nodes, 3 edges, 1 facet, 1 volume) (#2).
Quadrangle
Quadrangle (4 nodes, 4 edges, 1 facet, 1 volume) (#3).
Tetrahedron
Tetrahedron (4 nodes, 6 edges, 4 facets, 1 volume) (#4).
Hexahedron
Hexahedron (8 nodes, 12 edges, 6 facets, 1 volume) (#5).
Prism
Prism (6 nodes, 9 edges, 5 facets, 1 volume) (#6).
Pyramid
Pyramid (5 nodes, 8 edges, 5 facets, 1 volume) (#7).
Point
Point (1 node) (#15).
Note:
Next: Types for Resolution, Previous: Types for Integration, Up: Types for objects [Contents][Index]
Formulationformulation-type:
FemEquation
Finite element method formulation (all methods of moments, integral methods).
local-term-type:
Integral
Integral of Galerkin or Petrov-Galerkin type.
deRham
deRham projection (collocation).
quantity-type:
Local
Local quantity defining a field in a function space. In case a subspace is
considered, its identifier has to be given between the brackets following
the NameOfSpace function-space-id.
Global
Global quantity defining a global quantity from a function space. The
identifier of this quantity has to be given between the brackets following
the NameOfSpace function-space-id.
Integral
Integral quantity obtained by the integration of a
LocalQuantity before its use in an Equation term.
term-op-type:
Dt
Time derivative applied to the whole term of the equation. (Not implemented yet.)
DtDof
Time derivative applied only to the Dof{} term of the equation.
DtDt
Time derivative of 2nd order applied to the whole term of the equation. (Not implemented yet.)
DtDtDof
Time derivative of 2nd order applied only to the Dof{} term of the
equation.
Eig
The term is multiplied by (a certain function of) the eigenvalue. This
is to be used with the GenerateSeparate and EigenSolve
Resolution operations. An optional Order expression;
or Rational expression; statement can be added in the term
to specify the eigenvalue function. Full documentation of this feature
is not available yet.
JacNL
Nonlinear part of the Jacobian matrix (tangent stiffness matrix) to be assembled for nonlinear analysis.
DtDofJacNL
Nonlinear part of the Jacobian matrix for the first order time derivative (tangent mass matrix) to be assembled for nonlinear analysis.
NeverDt
No time scheme applied to the term (e.g., Theta is always 1 even if a theta scheme is applied).
Next: Types for PostProcessing, Previous: Types for Formulation, Up: Types for objects [Contents][Index]
Resolutionresolution-op:
Generate
[system-id]
Generate the system of equations system-id.
Solve
[system-id]
Solve the system of equations system-id.
SolveAgain
[system-id]
Save as Solve, but reuses the preconditionner when called
multiple times.
SetGlobalSolverOptions
[char-expression]
Set global PETSc solver options (with the same syntax as PETSc options
specified on the command line, e.g. "-ksp_type gmres -pc_type ilu").
GenerateJac
[system-id]
Generate the system of equations system-id using a jacobian matrix (of which the unknowns are corrections dx of the current solution x).
SolveJac
[system-id]
Solve the system of equations system-id using a jacobian matrix (of which the unknowns are corrections dx of the current solution x). Then, Increment the solution (x=x+dx) and compute the relative error dx/x.
GenerateSeparate
[system-id]
Generate matrices separately for DtDtDof, DtDof and
NoDt terms in system-id. The separate matrices can be used
with the Update operation (for efficient time domain analysis of
linear PDEs with constant coefficients), or with the EigenSolve
operation (for solving generalized eigenvalue problems).
GenerateOnly
[system-id, expression-cst-list]
Not documented yet.
GenerateOnlyJac
[system-id, expression-cst-list]
Not documented yet.
GenerateGroup
Not documented yet.
GenerateRightHandSideGroup
Not documented yet.
Update
[system-id]
Update the system of equations system-id (built from sub-matrices
generated separately with GenerateSeparate) with the
TimeFunction(s) provided in Assign constraints. This
assumes that the problem is linear, that the matrix coefficients are
independent of time, and that all sources are imposed using
Assign constraints.
Update
[system-id, expression]
Update the system of equations system-id (built from sub-matrices
generated separately with GenerateSeparate) with
expression. This assumes that the problem is linear, that the
matrix coefficients are independent of time, and that the
right-hand-side of the linear system can simply be multiplied by
expression at each step.
UpdateConstraint
[system-id, group-id, constraint-type]
Recompute the constraint of type constraint-type acting on group-id during processing.
GetResidual
[system-id, $variable-id]
Compute the residual r = b - A x and store its L2 norm in the
run-time variable $variable-id.
GetNormSolution | GetNormRightHandSide | GetNormResidual | GetNormIncrement
[system-id, $variable-id]
Compute the norm of the solution (resp. right-hand-side, residual or increment) and store its L2 norm in the run-time variable $variable-id.
SwapSolutionAndResidual
[system-id]
Swap the solution x and residual r vectors.
SwapSolutionAndRightHandSide
[system-id]
Swap the solution x and right-hand-side b vectors.
InitSolution
[system-id]
Creates a new solution vector, adds it to the solution vector list for
system-id, and initializes the solution. The values in the vector
are initialized to the values given in a Constraint of
Init type (if two values are given in Init, the second
value is used). If no constraint is provided, the values are initialized
to zero if the solution vector is the first in the solution list;
otherwise the values are initialized using the previous solution in the
list.
InitSolution1
[system-id]
Same as InitSolution, but uses the first value given in the
Init constraints.
CreateSolution
[system-id]
Creates a new solution vector, adds it to the solution vector list for system-id, and initializes the solution to zero.
CreateSolution
[system-id, expression-cst]
Same as CreateSolution, but initialize the solution by copying
the expression-cstth solution in the solution list.
Apply
[system-id]
x <- Ax
SetSolutionAsRightHandSide
[system-id]
b <- x
SetRightHandSideAsSolution
[system-id]
x <- b
Residual
[system-id]
res <- b - Ax
CopySolution
[system-id, char-expression | constant-id() ]
Copy the current solution x into a vector named
char-expression or into a list named constant-id.
CopySolution
[char-expression | constant-id(), system-id]
Copy the vector named char-expression or the list named
constant-id into the current solution x.
CopyRightHandSide
[system-id, char-expression | constant-id() ]
Copy the current right-hand side b into a vector named
char-expression or into a list named constant-id.
CopyRightHandSide
[char-expression | constant-id(), system-id]
Copy the vector named char-expression or the list named
constant-id into the current right-hand-side b.
CopyResidual
[system-id, char-expression | constant-id() ]
Copy the current residual into a vector named char-expression or into a list named constant-id.
CopyResidual
[char-expression | constant-id(), system-id]
Copy the vector named char-expression or the list named constant-id into the current residual.
SaveSolution
[system-id]
Save the solution of the system of equations system-id.
SaveSolutions
[system-id]
Save all the solutions available for the system of equations
system-id. This should be used with algorithms that generate more than
one solution at once, e.g., EigenSolve or FourierTransform.
RemoveLastSolution
[system-id]
Removes the last solution (i.e. associated with the last time step) associated with system system-id.
TransferSolution
[system-id]
Transfer the solution of system system-id, as an Assign
constraint, to the system of equations defined with a
DestinationSystem command. This is used with the
AssignFromResolution constraint type (see Types for Constraint).
Evaluate
[expression <, expression>]
Evaluate the expression(s).
SetTime
[expression]
Change the current time.
SetTimeStep
[expression]
Change the current time step number (1, 2, 3, ...)
SetDTime
[expression]
Change the current time step value (dt).
SetFrequency
[system-id, expression]
Change the frequency of system system-id.
SystemCommand
[expression-char]
Execute the system command given by expression-char.
Error
[expression-char]
Output error message expression-char.
Test
[expression] { resolution-op }
If expression is true (nonzero), perform the operations in resolution-op.
Test
[expression] { resolution-op } { resolution-op }
If expression is true (nonzero), perform the operations in the first resolution-op, else perform the operations in the second resolution-op.
While
[expression] { resolution-op }
While expression is true (nonzero), perform the operations in resolution-op.
Break
[]
Aborts an iterative loop, a time loop or a While loop.
Exit
[]
Exit, brutally.
Sleep
[expression]
Sleeps for expression seconds;
SetExtrapolationOrder
[expression-cst]
Chooses the extrapolation order to compute the initialization of the solution vector in time loops. Default is 0.
Print
[ { expression-list } <, File expression-char > <, Format expression-char > ]
Print the expressions listed in expression-list. If Format
is given, use it to format the (scalar) expressions like Printf.
Print
[ system-id <, File expression-char > <, { expression-cst-list } >
<, TimeStep { expression-cst-list } >]
Print the system system-id. If the expression-cst-list is given,
print only the values of the degrees of freedom given in that list.
If the TimeStep option is present, limit the printing to the selected
time steps.
EigenSolve
[system-id, expression-cst, expression-cst, expression-cst < , expression > ]
Eigenvalue/eigenvector computation using Arpack or SLEPc. The parameters
are: the system (which has to be generated with
GenerateSeparate[]), the number of eigenvalues/eigenvectors to
compute and the real and imaginary spectral shift (around which to look
for eigenvalues). The last optional argument allows to filter which
eigenvalue/eigenvector pairs will be saved. For example,
($EigenvalueReal > 0) would only keep pairs corresponding to
eigenvalues with a striclty positive real part.
Lanczos
[system-id, expression-cst, { expression-cst-list } , expression-cst]
Eigenvalue/eigenvector computation using the Lanczos algorithm. The
parameters are: the system (which has to be generated with
GenerateSeparate[]), the size of the Lanczos space, the indices
of the eigenvalues/eigenvectors to store, the spectral shift. This
routine is deprecated: use EigenSolve instead.
FourierTransform
[system-id, system-id, { expression-cst-list }]
On-the-fly (incremental) computation of a Fourier transform. The
parameters are: the (time domain) system, the destination system in
which the result of the Fourier tranform is to be saved (it should be
declared with Type Complex) and the list of frequencies to
consider. The computation is an approximation that assumes that the time
step is constant; it is not an actual Discrete Fourier Transform (the
number of samples is unknown a priori).
TimeLoopTheta
[expression-cst,expression-cst,expression,expression-cst]
{ resolution-op }
Time loop of a theta scheme. The parameters are: the initial time, the end time, the time step and the theta parameter (e.g., 1 for implicit Euler, 0.5 for Crank-Nicholson).
Warning: GetDP automatically handles time-dependent constraints when
they are provided using the TimeFunction mechanism in an
Assign-type Constraint (see Constraint). However,
GetDP cannot automatically transform general time-dependent source terms
in weak formulations (time-dependent functions written in a
Integral term). Such source terms will be correctly treated only
for implicit Euler, as the expression in the Integral term is
evaluated at the current time step. For other schemes, the source term
should be written explicitly, by splitting it in two (theta f_n+1
+ (1-theta) f_n), making use of the AtAnteriorTimeStep[] for the
second part, and specifying NeverDt in the Integral term.
TimeLoopNewmark
[expression-cst,expression-cst,expression,expression-cst,expression-cst]
{ resolution-op }
Time loop of a Newmark scheme. The parameters are: the initial time, the end time, the time step, the beta and the gamma parameter.
Warning: same restrictions apply for time-dependent functions in the
weak formulations as for TimeLoopTheta.
TimeLoopAdaptive
[expression-cst,expression-cst,expression-cst,expression-cst,
expression-cst,integration-method,<expression-cst-list>,
System { {system-id,expression-cst,expression-cst,norm-type} ... } |
PostOperation { {post-operation-id,expression-cst,expression-cst,norm-type}
... } ]
{ resolution-op }
{ resolution-op }
Time loop with variable time steps. The step size is adjusted according the local
truncation error (LTE) of the specified Systems/PostOperations via a predictor-corrector
method.
The parameters are: start time, end time, initial time step, min. time step,
max. time step, integration method, list of breakpoints (time points to be hit).
The LTE calculation can be based on all DOFs of a system and/or on a PostOperation
result. The parameters here are: System/PostOperation for LTE assessment, relative
LTE tolerance, absolute LTE tolerance, norm-type for LTE calculation.
Possible choices for integration-method are: Euler, Trapezoidal, Gear_2,
Gear_3, Gear_4, Gear_5, Gear_6.
The Gear methods correspond to backward differentiation formulas of
order 2..6.
Possible choices for norm-type: L1Norm, MeanL1Norm, L2Norm,
MeanL2Norm, LinfNorm.
MeanL1Norm and MeanL2Norm correspond to L1Norm and
L2Norm divided by the number of degrees of freedom, respectively.
The first resolution-op is executed every time step. The second one is
only executed if the actual time step is accepted (LTE is in the specified range).
E.g. SaveSolution[] is usually placed in the 2nd resolution-op.
IterativeLoop
[expression-cst,expression,expression-cst<,expression-cst>]
{ resolution-op }
Iterative loop for nonlinear analysis. The parameters are: the maximum number of iterations (if no convergence), the relative error to achieve and the relaxation factor (multiplies the iterative correction dx). The optional parameter is a flag for testing purposes.
IterativeLoopN
[expression-cst,expression,
System { {system-id,expression-cst,expression-cst,
assessed-object norm-type} ... } |
PostOperation { {post-operation-id,expression-cst,expression-cst,
norm-type} ... } ]
{ resolution-op }
Similar to IterativeLoop[] but allows to specify in detail the
tolerances and the type of norm to be calculated for convergence assessment.
The parameters are: the maximum number of iterations (if no convergence),
the relaxation factor (multiplies the iterative correction dx).
The convergence assessment can be based on all DOFs of a system and/or on a
PostOperation result. The parameters here are: System/PostOperation for
convergence assessment, relative tolerance, absolute tolerance,
assessed object (only applicable for a specified system), norm-type for
error calculation.
Possible choices for assessed-object: Solution, Residual,
RecalcResidual. Residual assesses the residual from the last iteration
whereas RecalcResidual calculates the residual once again after each
iteration. This means that with Residual usually one extra iteration is
performed, but RecalcResidual causes higher computational effort per
iteration. Assessing the residual can only be used for Newton’s method.
Possible choices for norm-type: L1Norm, MeanL1Norm, L2Norm,
MeanL2Norm, LinfNorm.
MeanL1Norm and MeanL2Norm correspond to L1Norm and
L2Norm divided by the number of degrees of freedom, respectively.
IterativeLinearSolver
Generic iterative linear solver. To be documented.
PostOperation
[post-operation-id]
Perform the specified PostOperation.
GmshRead
[expression-char]
When GetDP is linked with the Gmsh library, read a file using Gmsh. This
file can be in any format recognized by Gmsh. If the file contains one
or multiple post-processing fields, these fields will be evaluated using
the built-in Field[], ScalarField[], VectorField[],
etc., functions (see Miscellaneous functions).
(Note that GmshOpen and GmshMerge can be used instead of
GmshRead to force Gmsh to do classical “open” and “merge”
operations, instead of trying to “be intelligent” when reading
post-processing datasets, i.e., creating new models on the fly if
necessary.)
GmshRead
[expression-char, expression-cst]
Same thing as the GmshRead command above, except that the field
is forced to be stored with the given tag. The tag can be used to
retrieve the given field with the built-in Field[],
ScalarField[], VectorField[], etc., functions
(see Miscellaneous functions).
GmshRead
[expression-char,
$string]
Same as the GmshRead, but evaluates expression-char by
replacing a double precision format specifier with the value of the runtime
variable $string.
GmshWrite
[expression-char, expression-cst]
Writes the a Gmsh field to disk. (The format is guessed from the file extension.)
GmshClearAll
[]
Clears all Gmsh data (loaded with GmshRead and friends).
DeleteFile
[expression-char]
Delete a file.
RenameFile
[expression-char, expression-char]
Rename a file.
CreateDir | CreateDirectory
[expression-char]
Create a directory.
MPI_SetCommSelf
[]
Changes MPI communicator to self.
MPI_SetCommWorld
[]
Changes MPI communicator to world.
MPI_Barrier
[]
MPI barrier (blocks until all processes have reached this call).
MPI_BroadcastFields
[ < expression-list > ]
Broadcast all fields over MPI (except those listed in the list).
MPI_BroadcastVariables
[]
Broadcast all runtime variables over MPI.
Next: Types for PostOperation, Previous: Types for Resolution, Up: Types for objects [Contents][Index]
PostProcessingpost-value:
Local
{ local-value }
To compute a local quantity.
Integral
{ integral-value }
To integrate the expression over each element.
Previous: Types for PostProcessing, Up: Types for objects [Contents][Index]
PostOperationprint-support:
OnElementsOf
group-def
To compute a quantity on the elements belonging to the region group-def, where the solution was computed during the processing stage.
OnRegion
group-def
To compute a global quantity associated with the region group-def.
OnGlobal
To compute a global integral quantity, with no associated region.
OnSection
{ { expression-cst-list } { expression-cst-list } { expression-cst-list } }
To compute a quantity on a section of the mesh defined by three points (i.e., on the intersection of the mesh with a cutting a plane, specified by three points). Each expression-cst-list must contain exactly three elements (the coordinates of the points).
OnGrid
group-def
To compute a quantity in elements of a mesh which differs from the real
support of the solution. OnGrid group-def differs from
OnElementsOf group-def by the reinterpolation that must be
performed.
OnGrid
{ expression, expression, expression }
{ expression-cst-list-item | { expression-cst-list } ,
expression-cst-list-item | { expression-cst-list } ,
expression-cst-list-item | { expression-cst-list } }
To compute a quantity on a parametric grid. The three expressions
represent the three cartesian coordinates x, y and z, and
can be functions of the current values $A, $B and
$C. The values for $A, $B and $C are specified
by each expression-cst-list-item or expression-cst-list. For
example, OnGrid {Cos[$A], Sin[$A], 0} { 0:2*Pi:Pi/180, 0, 0 } will
compute the quantity on 360 points equally distributed on a circle in the
z=0 plane, and centered on the origin.
OnPoint
{ expression-cst-list }
To compute a quantity at a point. The expression-cst-list must contain exactly three elements (the coordinates of the point).
OnLine
{ { expression-cst-list } { expression-cst-list } } { expression-cst }
To compute a quantity along a line (given by its two end points), with an associated number of divisions equal to expression-cst. The interpolation points on the line are equidistant. Each expression-cst-list must contain exactly three elements (the coordinates of the points).
OnPlane
{ { expression-cst-list } { expression-cst-list } { expression-cst-list } }
{ expression-cst, expression-cst }
To compute a quantity on a plane (specified by three points), with an associated number of divisions equal to each expression-cst along both generating directions. Each expression-cst-list must contain exactly three elements (the coordinates of the points).
OnBox
{ { expression-cst-list } { expression-cst-list } { expression-cst-list }
{ expression-cst-list } } { expression-cst, expression-cst, expression-cst }
To compute a quantity in a box (specified by four points), with an associated number of divisions equal to each expression-cst along the three generating directions. Each expression-cst-list must contain exactly three elements (the coordinates of the points).
print-option:
File
expression-char
Outputs the result in a file named expression-char.
File
> expression-char
Same as File expression-char, except that, if several File >
expression-char options appear in the same PostOperation, the results
are concatenated in the file expression-char.
File
>> expression-char
Appends the result to a file named expression-char.
AppendToExistingFile
expression-cst
Appends the result to the file specified with File. (Same
behavior as > if expression-cst = 1; same behavior as
>> if expression-cst = 2.)
Name | Label
expression-char
For formats that support it, sets the label of the output field to
expression-char (also used with with SendToServer to force
the label).
Depth
expression-cst
Recursive division of the elements if expression-cst is greater than zero, derefinement if expression-cst is smaller than zero. If expression-cst is equal to zero, evaluation at the barycenter of the elements.
AtGaussPoints
expression-cst
Print result at the specified number of Gauss points.
Skin
Computes the result on the boundary of the region.
Smoothing
< expression-cst >
Smoothes the solution at the nodes.
HarmonicToTime
expression-cst
Converts a harmonic solution into a time-dependent one (with expression-cst steps).
Dimension
expression-cst
Forces the dimension of the elements to consider in an element search. Specifies the problem dimension during an adaptation (h- or p-refinement).
TimeStep
expression-cst-list-item | { expression-cst-list }
Outputs results for the specified time steps only.
TimeValue
expression-cst-list-item | { expression-cst-list }
Outputs results for the specified time value(s) only.
TimeImagValue
expression-cst-list-item | { expression-cst-list }
Outputs results for the specified imaginary time value(s) only.
LastTimeStepOnly
Outputs results for the last time step only (useful when calling a
PostOperation directly in a Resolution, for example).
AppendExpressionToFileName
expression
Evaluate the given expression at run-time and append it to the filename.
AppendExpressionFormat
expression-char
C-style format string for printing the expression provided in
AppendExpressionToFileName. Default is "%.16g".
AppendTimeStepToFileName
< expression-cst >
Appends the time step to the output file; only makes sense with LastTimeStepOnly.
AppendStringToFileName
expression-char
Append the given expression-char to the filename.
OverrideTimeStepValue
expression-cst
Overrides the value of the current time step with the given value.
NoMesh
< expression-cst >
Prevents the mesh from being written in the output file (useful with new mesh-based solution formats).
SendToServer
expression-char
Send the value to the Onelab server, using expression-char as the parameter name.
SendToServer
expression-char { expression-cst-list }
Send the requested harmonics of the value to the Onelab server, using expression-char as the parameter name.
Color
expression-char
Used with SendToServer, sets the color of the parameter in the
Onelab server.
Hidden
< expression-cst >
Used with SendToServer, selects the visibility of the exchanged value.
Closed
expression-char
Used with SendToServer, closes (or opens) the subtree containing
the parameter.
Units
expression-char
Used with SendToServer, sets the units of the parameter in the
Onelab server.
Frequency
expression-cst-list-item | { expression-cst-list }
Outputs results for the specified frequencies only.
Format
post-operation-fmt
Outputs results in the specified format.
Adapt
P1 | H1 | H2
Performs p- or h-refinement on the post-processing result, considered as an error map.
Target
expression-cst
Specifies the target for the optimizer during adaptation (error for
P1|H1, number of elements for H2).
Value
expression-cst-list-item | { expression-cst-list }
Specifies acceptable output values for discrete optimization (e.g. the
available interpolation orders with Adapt P1).
Sort
Position | Connection
Sorts the output by position (x, y, z) or by connection (for LINE
elements only).
Iso
expression-cst
Outputs directly contour prints (with expression-cst values) instead of elementary values.
Iso
{ expression-cst-list }
Outputs directly contour prints for the values specified in the expression-cst-list instead of elementary values.
NoNewLine
Suppresses the new lines in the output when printing global quantities
(i.e., with Print OnRegion or Print OnGlobal).
ChangeOfCoordinates
{ expression, expression, expression }
Changes the coordinates of the results according to the three expressions
given in argument. The three expressions represent the three new
cartesian coordinates x, y and z, and can be functions of
the current values of the cartesian coordinates $X, $Y and
$Z.
ChangeOfValues
{ expression-list }
Changes the values of the results according to the expressions given in argument. The expressions represent the new values (x-compoment, y-component, etc.), and can be functions of the current values of the solution ($Val0, $Val1, etc.).
DecomposeInSimplex
Decomposes all output elements in simplices (points, lines, triangles or tetrahedra).
StoreInVariable
$expression-char
Stores the result of a point-wise evaluation or an OnRegion
post-processing operation in the run-time variable
$code[$]expression-char.
StoreInRegister
expression-cst
Stores the result of point-wise evaluation or an OnRegion
post-processing operation in the register expression-cst.
StoreMinInRegister
StoreMaxInRegister
expression-cst
Stores the minimum or maximum value of an OnElementsOf post-processing
operation in the register expression-cst.
StoreMinXinRegister
StoreMinYinRegister
StoreMinZinRegister
StoreMaxXinRegister
StoreMaxYinRegister
StoreMaxZinRegister
expression-cst
Stores the X, Y or Z coordinate of the location, where the minimum or maximum
of an OnElementsOf post-processing operation occurs, in the register
expression-cst.
StoreInField
expression-cst
Stores the result of a post-processing operation in the field (Gmsh list-based post-processing view) with tag expression-cst.
StoreInMeshBasedField
expression-cst
Stores the result of a post-processing operation in the mesh-based field (Gmsh mesh-based post-processing view) with tag expression-cst.
TimeLegend
< { expression, expression, expression } >
Includes a time legend in Gmsh plots. If the three optional expressions giving the position of the legend are not specified, the legend is centered on top of the plot.
FrequencyLegend
< { expression, expression, expression } >
Includes a frequency legend in Gmsh plots. If the three optional expressions giving the position of the legend are not specified, the legend is centered on top of the plot.
EigenvalueLegend
< { expression, expression, expression } >
Includes an eigenvalue legend in Gmsh plots. If the three optional expressions giving the position of the legend are not specified, the legend is centered on top of the plot.
post-operation-fmt:
Gmsh
GmshParsed
Gmsh output. See Input file format and the documentation of Gmsh (http://gmsh.info) for a description of the file formats.
Table
Space oriented column output, e.g., suitable for Gnuplot, Excel, Caleida
Graph, etc. The columns are: element-type element-index
x-coord y-coord z-coord <x-coord y-coord
z-coord> … real real real values. The
three real numbers preceding the values contain
context-dependent information, depending on the type of plot: curvilinear
abscissa for OnLine plots, normal to the plane for OnPlane
plots, parametric coordinates for parametric OnGrid plots, etc.
SimpleTable
Like Table, but with only the x-coord y-coord
z-coord and values columns.
TimeTable
Time oriented column output, e.g., suitable for Gnuplot, Excel, Caleida Graph, etc. The columns are: time-step time x-coord y-coord z-coord <x-coord y-coord z-coord> … value.
NodeTable
Table of nodal values, in the form node-number
node-value(s). When exported to a file, the total number of nodal
values is printed first. The data is automatically exported as a
run-time accessible list as well as a ONELAB variable, with the name of
the PostOperation quantity. The values are also directly usable
by the ValueFromTable function, which allows to use them as
values in a nodal Constraint.
ElementTable
Table of element values, in the form element-number
element-node-value(s). When exported to a file, the total number
of element values is printed first. The data is automatically exported
as a run-time accessible list as well as a ONELAB variable, with the
name of the PostOperation quantity. The values are also directly
usable by the ValueFromTable function, which allows to use them
as values in an element-wise Constraint.
Gnuplot
Space oriented column output similar to the Table format, except that
a new line is created for each node of each element, with a repetition of
the first node if the number of nodes in the element is greater than 2. This
permits to draw unstructured meshes and nice three-dimensional elevation
plots in Gnuplot. The columns are: element-type element-index
x-coord y-coord z-coord real real real
values. The three real numbers preceding the values
contain context-dependent information, depending on the type of plot:
curvilinear abscissa for OnLine plots, normal to the plane for
OnPlane plots, parametric coordinates for parametric OnGrid
plots, etc.
Adaptation
Adaptation map, suitable for the GetDP -adapt command line option.
Next: Complete examples, Previous: Types for objects, Up: Top [Contents][Index]
Next: Group examples, Previous: Short examples, Up: Short examples [Contents][Index]
The simplest constant expression consists of an integer or a real number as in
21 -3
or
-3.1415 27e3 -290.53e-12
Using operators and the classic math functions, constant-ids can be defined:
c1 = Sin[2/3*3.1415] * 5000^2; c2 = -1/c1;
Next: Function examples, Previous: Constant expression examples, Up: Short examples [Contents][Index]
Group examplesLet us assume that some elements in the input mesh have the region numbers 1000, 2000 and 3000. In the definitions
Group {
Air = Region[1000]; Core = Region[2000]; Inductor = Region[3000];
NonConductingDomain = Region[{Air, Core}];
ConductingDomain = Region[{Inductor}];
}
Air, Core, Inductor are identifiers of elementary
region groups while NonConductingDomain and
ConductingDomain are global region groups.
Groups of function type contain lists of entities built on the region groups appearing in their arguments. For example,
NodesOf[NonConductingDomain]
represents the group of nodes of geometrical elements belonging to the regions
in NonConductingDomain and
EdgesOf[DomainC, Not SkinDomainC]
represents the group of edges of geometrical elements belonging to the regions
in DomainC but not to those of SkinDomainC.
Next: Constraint examples, Previous: Group examples, Up: Short examples [Contents][Index]
Function examplesA physical characteristic is a piecewise defined function. The magnetic
permeability mu[] can for example be defined in the considered
regions by
Function {
mu[Air] = 4.e-7*Pi;
mu[Core] = 1000.*4.e-7*Pi;
}
A nonlinear characteristic can be defined through an expression with arguments, e.g.,
Function {
mu0 = 4.e-7*Pi;
a1 = 1000.; b1 = 100.; // Constants
mu[NonlinearCore] = mu0 + 1./(a1+b1*Norm[$1]^6);
}
where function mu[] in region NonLinearCore has one argument
$1 which has to be the magnetic flux density. This function is
actually called when writing the equations of a formulation, which permits
to directly extend it to a nonlinear form by adding only the necessary
arguments. For example, in a magnetic vector potential formulation, one may
write mu[{Curl a}] instead of mu[] in Equation terms
(see Formulation examples). Multiple arguments can be specified in a
similar way: writing mu[{Curl a},{T}] in an Equation term
will provide the function mu[] with two usable arguments, $1
(the magnetic flux density) and $2 (the temperature).
It is also possible to directly interpolate one-dimensional functions from tabulated data. In the following example, the function f(x) as well as its derivative f’(x) are interpolated from the (x,f(x)) couples (0,0.65), (1,0.72), (2,0.98) and (3,1.12):
Function {
couples = {0, 0.65 , 1, 0.72 , 2, 0.98 , 3, 1.12};
f[] = InterpolationLinear[$1]{List[couples]};
dfdx[] = dInterpolationLinear[$1]{List[couples]};
}
The function f[] may then be called in an Equation
term of a Formulation with one argument, x. Notice how the list
of constants List[couples] is supplied as a list of parameters to the
built-in function InterpolationLinear (see Constants, as well as
Functions). In order to facilitate the construction of such
interpolations, the couples can also be specified in two separate lists,
merged with the alternate list ListAlt command (see Constants):
Function {
data_x = {0, 1, 2, 3};
data_f = {0.65, 0.72, 0.98, 1.12};
f[] = InterpolationLinear[$1]{ListAlt[data_x, data_f]};
dfdx[] = dInterpolationLinear[$1]{ListAlt[data_x, data_f]};
}
In order to optimize the evaluation time of complex expressions,
registers may be used (see Run-time variables and registers). For
example, the evaluation of g[] = f[$1]*Sin[f[$1]^2] would require
two (costly) linear interpolations. But the result of the evaluation of
f[] may be stored in a register (for example the register 0) with
g[] = f[$1]#0 * Sin[#0^2];
thus reducing the number of evaluations of f[] (and of the
argument $1) to one.
The same results can be obtained using a run-time variable $v:
g[] = ($v = f[$1]) * Sin[$v^2];
A function can also be time dependent, e.g.,
Function {
Freq = 50.; Phase = 30./180.*Pi; // Constants
TimeFct_Sin[] = Sin [ 2.*Pi*Freq * $Time + Phase ];
TimeFct_Exp[] = Exp [ - $Time / 0.0119 ];
TimeFct_ExtSin[] = Sin_wt_p [] {2.*Pi*Freq, Phase};
}
Note that TimeFct_ExtSin[] is identical to TimeFct_Sin[] in a
time domain analysis, but also permits to define phasors implicitely in the
case of harmonic analyses.
Next: FunctionSpace examples, Previous: Function examples, Up: Short examples [Contents][Index]
Constraint examplesConstraints are referred to in FunctionSpaces and are usually used
for boundary conditions (Assign type).
For example, essential conditions on two surface regions,
Surf0 and Surf1, will be first defined by
Constraint {
{ Name DirichletBoundaryCondition1; Type Assign;
Case {
{ Region Surf0; Value 0.; }
{ Region Surf1; Value 1.; }
}
}
}
The way the Values are associated with Regions (with their
nodes, their edges, their global regions, …) is defined in the
FunctionSpaces which use the Constraint. In other words, a
Constraint defines data but does not define the method to process
them. A time dependent essential boundary condition on Surf1 would be
introduced as (cf. Function examples for the definition of
TimeFct_Exp[]):
{ Region Surf1; Value 1.; TimeFunction 3*TimeFct_Exp[] }
It is important to notice that the time dependence cannot be
introduced in the Value field, since the Value is only
evaluated once during the pre-processing.
Other constraints can be referred to in Formulations. It is the case of
those defining electrical circuit connections (Network type), e.g.,
Constraint {
{ Name ElectricalCircuit; Type Network;
Case Circuit1 {
{ Region VoltageSource; Branch {1,2}; }
{ Region PrimaryCoil; Branch {1,2}; }
}
Case Circuit2 {
{ Region SecondaryCoil; Branch {1,2}; }
{ Region Charge; Branch {1,2}; }
}
}
}
which defines two non-connected circuits (Circuit1 and Circuit2),
with an independent numbering of nodes: region VoltageSource is connected in
parallel with region PrimaryCoil, and region SecondaryCoil is
connected in parallel with region Charge.
Next: Jacobian examples, Previous: Constraint examples, Up: Short examples [Contents][Index]
FunctionSpace examplesVarious discrete function spaces can be defined in the frame of the finite element method.
| • Conform space | ||
| • High order space | ||
| • Global values | ||
| • Curl-conform space | ||
| • Gauge condition | ||
| • Coupled spaces | ||
| • Multiply connected domains |
Next: High order space, Previous: FunctionSpace examples, Up: FunctionSpace examples [Contents][Index]
The most elementary function space is the nodal finite element space, defined on a mesh of a domain W and denoted S0(W) (associated finite elements can be of various geometries), and associated with essential boundary conditions (Dirichlet conditions). It contains 0-forms, i.e., scalar fields of potential type:
v = Sum [ vn * sn, for all n in N ], v in S0(W)
where N is the set of nodes of W, sn is the nodal basis function associated with node n and vn is the value of v at node n. It is defined by
FunctionSpace {
{ Name Hgrad_v; Type Form0;
BasisFunction {
{ Name sn; NameOfCoef vn; Function BF_Node;
Support Domain; Entity NodesOf[All]; }
}
Constraint {
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint DirichletBoundaryCondition1; }
}
}
}
Function sn is the built-in basis function BF_Node associated with
all nodes (NodesOf) in the mesh of W (Domain). Previously
defined Constraint DirichletBoundaryCondition1
(see Constraint examples) is used as boundary condition.
In the example above, Entity NodesOf[All] is preferred to
Entity NodesOf[Domain].
In this way, the list of all the nodes of Domain will not have to be
generated. All the nodes of each geometrical element in Support Domain
will be directly taken into account.
Next: Global values, Previous: Conform space, Up: FunctionSpace examples [Contents][Index]
Higher order finite elements can be directly taken into account by BF_Node.
Hierarchical finite elements for 0-forms can be used by simply adding other basis
functions (associated with other geometrical entities, e.g., edges and facets) to
BasisFunction, e.g.,
…
BasisFunction {
{ Name sn; NameOfCoef vn; Function BF_Node;
Support Domain; Entity NodesOf[All]; }
{ Name s2; NameOfCoef v2; Function BF_Node_2E;
Support Domain; Entity EdgesOf[All]; }
}
…
Next: Curl-conform space, Previous: High order space, Up: FunctionSpace examples [Contents][Index]
A scalar potential with floating values vf on certain boundaries Gf, f in Cf, e.g., for electrostatic problems, can be expressed as
v = Sum [ vn * sn, for all n in Nv ] + Sum [ vf * sf, for all f in Cf ], v in S0(W)
where Nv is the set of inner nodes of W and each function sf
is associated with the group of nodes of boundary Gf, f in Cf
(SkinDomainC); sf is the sum of the nodal basis functions
of all the nodes of Cf. Its function space is defined by
FunctionSpace {
{ Name Hgrad_v_floating; Type Form0;
BasisFunction {
{ Name sn; NameOfCoef vn; Function BF_Node;
Support Domain; Entity NodesOf[All, Not SkinDomainC]; }
{ Name sf; NameOfCoef vf; Function BF_GroupOfNodes;
Support Domain; Entity GroupsOfNodesOf[SkinDomainC]; }
}
GlobalQuantity {
{ Name GlobalElectricPotential; Type AliasOf; NameOfCoef vf; }
{ Name GlobalElectricCharge; Type AssociatedWith;
NameOfCoef vf; }
}
Constraint { … }
}
}
Two global quantities have been associated with this space: the electric
potential GlobalElectricPotential, being an alias of
coefficient vf, and the electric charge
GlobalElectricCharge, being associated with coefficient
vf.
Next: Gauge condition, Previous: Global values, Up: FunctionSpace examples [Contents][Index]
Another space is the edge finite element space, denoted S1(W), containing 1-forms, i.e., curl-conform fields:
h = Sum [ he * se, for all e in E ], h in S1(W)
where E is the set of edges of W, se is the edge basis function for edge e and he is the circulation of h along edge e. It is defined by
FunctionSpace {
{ Name Hcurl_h; Type Form1;
BasisFunction {
{ Name se; NameOfCoef he; Function BF_Edge;
Support Domain; Entity EdgesOf[All]; }
}
Constraint { … }
}
}
Next: Coupled spaces, Previous: Curl-conform space, Up: FunctionSpace examples [Contents][Index]
A 1-form function space containing vector potentials can be associated
with a gauge condition, which can be defined as a constraint, e.g., a
zero value is fixed for all circulations along edges of a tree
(EdgesOfTreeIn) built in the mesh (Domain), having to be
complete on certain boundaries (StartingOn Surf):
Constraint {
{ Name GaugeCondition_a_Mag_3D; Type Assign;
Case {
{ Region Domain; SubRegion Surf; Value 0.; }
}
}
}
FunctionSpace {
{ Name Hcurl_a_Gauge; Type Form1;
BasisFunction {
{ Name se; NameOfCoef ae; Function BF_Edge;
Support Domain; Entity EdgesOf[All]; }
}
Constraint {
{ NameOfCoef ae;
EntityType EdgesOfTreeIn; EntitySubType StartingOn;
NameOfConstraint GaugeCondition_a_Mag_3D; }
…
}
}
}
Next: Multiply connected domains, Previous: Gauge condition, Up: FunctionSpace examples [Contents][Index]
A 1-form function space, containing curl free fields in certain regions WcC
(DomainCC) of W, which are the complementary part of Wc
(DomainC) in W, can be explicitly characterized by
h = Sum [ hk * sk, for all e in Ec ] + Sum [ phin * vn, for all n in NcC ], h in S1(W)
where Ec is the set of inner edges of W, NcC is the set of nodes inside WcC and on its boundary dWcC, sk is an edge basis function and vn is a vector nodal function. Such a space, coupling a vector field with a scalar potential, can be defined by
FunctionSpace {
{ Name Hcurl_hphi; Type Form1;
BasisFunction {
{ Name sk; NameOfCoef hk; Function BF_Edge;
Support DomainC; Entity EdgesOf[All, Not SkinDomainC]; }
{ Name vn; NameOfCoef phin; Function BF_GradNode;
Support DomainCC; Entity NodesOf[All]; }
{ Name vn; NameOfCoef phic; Function BF_GroupOfEdges;
Support DomainC; Entity GroupsOfEdgesOnNodesOf[SkinDomainC];}
}
Constraint {
{ NameOfCoef hk;
EntityType EdgesOf; NameOfConstraint MagneticField; }
{ NameOfCoef phin;
EntityType NodesOf; NameOfConstraint MagneticScalarPotential; }
{ NameOfCoef phic;
EntityType NodesOf; NameOfConstraint MagneticScalarPotential; }
}
}
}
This example points out the definition of a piecewise defined basis function, e.g.,
function vn being defined with BF_GradNode in DomainCC and
BF_GroupOfEdges in DomainC. This leads to an easy coupling
between these regions.
Previous: Coupled spaces, Up: FunctionSpace examples [Contents][Index]
In case a multiply connected domain WcC is considered, basis functions
associated with cuts (SurfaceCut) have to be added to the previous
basis functions, which gives the function space below:
Group {
_TransitionLayer_SkinDomainC_ =
ElementsOf[SkinDomainC, OnOneSideOf SurfaceCut];
}
FunctionSpace {
{ Name Hcurl_hphi; Type Form1;
BasisFunction {
… same as above …
{ Name sc; NameOfCoef Ic; Function BF_GradGroupOfNodes;
Support ElementsOf[DomainCC, OnOneSideOf SurfaceCut];
Entity GroupsOfNodesOf[SurfaceCut]; }
{ Name sc; NameOfCoef Icc; Function BF_GroupOfEdges;
Support DomainC;
Entity GroupsOfEdgesOf
[SurfaceCut,
InSupport _TransitionLayer_SkinDomainC_]; }
}
GlobalQuantity {
{ Name I; Type AliasOf ; NameOfCoef Ic; }
{ Name U; Type AssociatedWith; NameOfCoef Ic; }
}
Constraint {
… same as above …
{ NameOfCoef Ic;
EntityType GroupsOfNodesOf; NameOfConstraint Current; }
{ NameOfCoef Icc;
EntityType GroupsOfNodesOf; NameOfConstraint Current; }
{ NameOfCoef U;
EntityType GroupsOfNodesOf; NameOfConstraint Voltage; }
}
}
}
Global quantities associated with the cuts, i.e., currents and voltages if h is the magnetic field, have also been defined.
Next: Integration examples, Previous: FunctionSpace examples, Up: Short examples [Contents][Index]
Jacobian examplesA simple Jacobian method is for volume transformations (of n-D
regions in n-D geometries; n = 1, 2 or 3),
e.g., in region Domain,
Jacobian {
{ Name Vol;
Case {
{ Region Domain; Jacobian Vol; }
}
}
}
Jacobian VolAxi would define a volume Jacobian for axisymmetrical problems.
A Jacobian method can also be piecewise defined, in DomainInf, where
an infinite geometrical transformation has to be made using two constant
parameters (inner and outer radius of a spherical shell), and in all the
other regions (All, being the default); in each case, a volume
Jacobian is used. This method is defined by:
Jacobian {
{ Name Vol;
Case {
{ Region DomainInf; Jacobian VolSphShell {Val_Rint, Val_Rext}; }
{ Region All; Jacobian Vol; }
}
}
}
Next: Formulation examples, Previous: Jacobian examples, Up: Short examples [Contents][Index]
Integration examplesA commonly used numerical integration method is the Gauss integration,
with a number of integration points (NumberOfPoints) depending on
geometrical element types (GeoElement), i.e.
Integration {
{ Name Int_1;
Case { {Type Gauss;
Case { { GeoElement Triangle ; NumberOfPoints 4; }
{ GeoElement Quadrangle ; NumberOfPoints 4; }
{ GeoElement Tetrahedron; NumberOfPoints 4; }
{ GeoElement Hexahedron ; NumberOfPoints 6; }
{ GeoElement Prism ; NumberOfPoints 9; } }
}
}
}
}
The method above is valid for both 2D and 3D problems, for different kinds of elements.
Next: Resolution examples, Previous: Integration examples, Up: Short examples [Contents][Index]
Formulation examples| • Electrostatics | ||
| • Electrostatics 2 | ||
| • Magnetostatics | ||
| • Magnetodynamics | ||
| • Other formulations |
Next: Electrostatics 2, Previous: Formulation examples, Up: Formulation examples [Contents][Index]
An electrostatic formulation using an electric scalar potential v, i.e.
( epsr grad v, grad vp ) W = 0, for all vp in S0(W),
is expressed by
Formulation {
{ Name Electrostatics_v; Type FemEquation;
Quantity {
{ Name v; Type Local; NameOfSpace Hgrad_v; }
}
Equation {
Integral { [ epsr[] * Dof{Grad v} , {Grad v} ];
In Domain; Jacobian Vol; Integration Int_1; }
}
}
}
The density of the Integral term is a copy of the symbolic form of
the formulation, i.e., the product of a relative permittivity function
epsr[] by a vector of degrees of freedom (Dof{.}); the
scalar product of this with the gradient of test function v results
in a symmetrical matrix.
Note that another Quantity could be defined for test functions,
e.g., vp defined by { Name vp; Type Local; NameOfSpace
Hgrad_v; }. However, its use would result in the computation of a full
matrix and consequently in a loss of efficiency.
Next: Magnetostatics, Previous: Electrostatics, Up: Formulation examples [Contents][Index]
An extension of the formulation above can be made to take floating
potentials and electrical charges into account (the latter being defined in
FunctionSpace Hgrad_v_floating), i.e.
Formulation {
{ Name Electrostatics_v_floating; Type FemEquation;
Quantity {
{ Name v; Type Local; NameOfSpace Hgrad_v_floating; }
{ Name V; Type Global;
NameOfSpace Hgrad_v_floating [GlobalElectricPotential]; }
{ Name Q; Type Global;
NameOfSpace Hgrad_v_floating [GlobalElectricCharge]; }
}
Equation {
Integral { [ epsr[] * Dof{Grad v} , {Grad v} ];
In Domain; Jacobian Vol; Integration Int_1; }
GlobalTerm { [ - Dof{Q}/eps0 , {V} ]; In SkinDomainC; }
}
}
}
with the predefinition Function { eps0 = 8.854187818e-12; }.
Next: Magnetodynamics, Previous: Electrostatics 2, Up: Formulation examples [Contents][Index]
A magnetostatic 3D vector potential formulation
( nu curl a , curl ap ) W - ( js , ap ) Ws = 0, for all ap in S1(W) with gauge condition,
with a source current density js in inductors Ws, is expressed by
Formulation {
{ Name Magnetostatics_a_3D; Type FemEquation;
Quantity {
{ Name a; Type Local; NameOfSpace Hcurl_a_Gauge; }
}
Equation {
Integral { [ nu[] * Dof{Curl a} , {Curl a} ];
In Domain; Jacobian Vol; Integration Int_1; }
Integral { [ - SourceCurrentDensity[] , {a} ];
In DomainWithSourceCurrentDensity;
Jacobian Vol; Integration Int_1; }
}
}
}
Note that js is here given by a function SourceCurrentDensity[],
but could also be given by data computed from another problem,
e.g., from an electrokinetic problem (coupling of formulations) or
from a fully fixed function space (constraints fixing the density, which is
usually more efficient in time domain analyses).
Next: Other formulations, Previous: Magnetostatics, Up: Formulation examples [Contents][Index]
A magnetodynamic 3D or 2D h-phi formulation, i.e., coupling the magnetic field h with a magnetic scalar potential phi,
Dt ( mu h , hp ) W + ( ro curl h , curl hp ) Wc = 0, for all hp in S1(W),
can be expressed by
Formulation {
{ Name Magnetodynamics_hphi; Type FemEquation;
Quantity {
{ Name h; Type Local; NameOfSpace Hcurl_hphi; }
}
Equation {
Integral { Dt [ mu[] * Dof{h} , {h} ];
In Domain; Jacobian Vol; Integration Int_1; }
Integral { [ rho[] * Dof{Curl h} , {Curl h} ];
In DomainC; Jacobian Vol; Integration Int_1; }
}
}
}
Previous: Magnetodynamics, Up: Formulation examples [Contents][Index]
In case nonlinear physical characteristics are considered, arguments are
used for associated functions, e.g., mu[{h}]. Several test
functions can be considered in an Equation field. Consequently,
mixed formulations can be defined.
Next: PostProcessing examples, Previous: Formulation examples, Up: Short examples [Contents][Index]
Resolution examples| • Static resolution | ||
| • Frequency domain resolution | ||
| • Time domain resolution | ||
| • Nonlinear resolution | ||
| • Coupled formulations |
Next: Frequency domain resolution, Previous: Resolution examples, Up: Resolution examples [Contents][Index]
A static resolution, e.g., for the electrostatic formulation (see Formulation examples), can be defined by
Resolution {
{ Name Electrostatics_v;
System {
{ Name Sys_Ele; NameOfFormulation Electrostatics_v; }
}
Operation {
Generate[Sys_Ele]; Solve[Sys_Ele]; SaveSolution[Sys_Ele];
}
}
}
The generation (Generate) of the matrix of the system Sys_Ele
will be made with the formulation Electrostatics_v, followed by its
solving (Solve) and the saving of the solution (SaveSolution).
Next: Time domain resolution, Previous: Static resolution, Up: Resolution examples [Contents][Index]
A frequency domain resolution, e.g., for the magnetodynamic h-phi formulation (see Formulation examples), is given by
Resolution {
{ Name Magnetodynamics_hphi;
System {
{ Name Sys_Mag; NameOfFormulation Magnetodynamics_hphi;
Frequency Freq; }
}
Operation {
Generate[Sys_Mag]; Solve[Sys_Mag]; SaveSolution[Sys_Mag];
}
}
}
preceded by the definition of constant Freq, e.g.,
Function {
Freq = 50.;
}
Next: Nonlinear resolution, Previous: Frequency domain resolution, Up: Resolution examples [Contents][Index]
A time domain resolution, e.g., for the same magnetodynamic h-phi formulation (see Formulation examples), is given by
Resolution {
{ Name Magnetodynamics_hphi_Time;
System {
{ Name Sys_Mag; NameOfFormulation Magnetodynamics_hphi; }
}
Operation {
InitSolution[Sys_Mag]; SaveSolution[Sys_Mag];
TimeLoopTheta[Mag_Time0, Mag_TimeMax, Mag_DTime[], Mag_Theta[]] {
Generate[Sys_Mag]; Solve[Sys_Mag]; SaveSolution[Sys_Mag];
}
}
}
}
If, e.g., the Resolution above is preceded by the constant and function
definitions below
Function {
Tc = 10.e-3;
Mag_Time0 = 0.; Mag_TimeMax = 2.*Tc; Mag_DTime[] = Tc/20.;
Mag_Theta[] = 1./2.;
}
the performed time domain analysis will be a Crank-Nicolson scheme
(theta-scheme with Theta = 0.5) with initial time 0 ms, end time
20 ms and time step 1 ms.
Next: Coupled formulations, Previous: Time domain resolution, Up: Resolution examples [Contents][Index]
In case a nonlinear problem is solved, an iterative loop has to be defined in an appropriate level of the recursive resolution operations, e.g., for the magnetodynamic problem above,
…
Operation {
InitSolution[Sys_Mag]; SaveSolution[Sys_Mag];
TimeLoopTheta[Mag_Time0, Mag_TimeMax, Mag_DTime[], Mag_Theta[]] {
IterativeLoop[NL_NbrMax, NL_Eps, NL_Relax] {
GenerateJac[Sys_Mag]; SolveJac[Sys_Mag];
}
SaveSolution[Sys_Mag];
}
}
…
preceded by constant definitions, e.g.,
Function {
NL_Eps = 1.e-4; NL_Relax = 1.; NL_NbrMax = 80;
}
Previous: Nonlinear resolution, Up: Resolution examples [Contents][Index]
A coupled problem, e.g., magnetodynamic (in frequency domain;
Frequency Freq) - thermal (in time domain) coupling, with temperature
dependent characteristics (e.g., rho[{T}], …), can be defined by:
Resolution {
{ Name MagnetoThermalCoupling_hphi_T;
System {
{ Name Sys_Mag; NameOfFormulation Magnetodynamics_hphi;
Frequency Freq; }
{ Name Sys_The; NameOfFormulation Thermal_T; }
}
Operation {
InitSolution[Sys_Mag]; InitSolution[Sys_The];
IterativeLoop[NL_NbrMax, NL_Eps, NL_Relax] {
GenerateJac[Sys_Mag]; SolveJac[Sys_Mag];
GenerateJac[Sys_The]; SolveJac[Sys_The];
}
SaveSolution[Sys_Mag]; SaveSolution[Sys_The];
}
}
}
Two systems of equations, Sys_Mag and Sys_The, will be solved
iteratively until convergence (Criterion), using a relaxation factor
(RelaxationFactor).
It can be seen through these examples that many resolutions can be linked or nested directly by the user, which gives a great freedom for coupled problems.
Next: PostOperation examples, Previous: Resolution examples, Up: Short examples [Contents][Index]
PostProcessing examplesThe quantities to be post-computed based on a solution of a resolution are
defined, e.g., for the electrostatic problem (see Formulation examples;
see Resolution examples), for the solution associated with the
formulation Electrostatics_v, by
PostProcessing {
{ Name EleSta_v; NameOfFormulation Electrostatics_v;
Quantity {
{ Name v; Value { Local { [ {v} ]; In Domain; } } }
{ Name e; Value { Local { [ -{Grad v} ]; In Domain; } } }
{ Name d; Value { Local { [ -eps0*epsr[] *{Grad v} ];
In Domain; } } }
}
}
}
The electric scalar potential v (v), the electric field
e (e) and the electric flux density d (d) can
all be computed from the solution. They are all defined in the region
Domain.
The quantities for the solution associated with the formulation
Electrostatics_v_floating are defined by
PostProcessing {
{ Name EleSta_vf; NameOfFormulation Electrostatics_v_floating;
Quantity {
… same as above …
{ Name Q; Value { Local { [ {Q} ]; In SkinDomainC; } } }
{ Name V; Value { Local { [ {V} ]; In SkinDomainC; } } }
}
}
}
which points out the way to define post-quantities based on global quantities.
Previous: PostProcessing examples, Up: Short examples [Contents][Index]
PostOperation examplesThe simplest post-processing operation is the generation of maps of local
quantities, i.e., the display of the computed fields on the mesh. For
example, using the PostProcessing defined in PostProcessing examples, the maps of the electric scalar potential and of the electric
field on the elements of the region Domain are defined as:
PostOperation {
{ Name Map_v_e; NameOfPostProcessing EleSta_v ;
Operation {
Print [ v, OnElementsOf Domain, File "map_v.pos" ];
Print [ e, OnElementsOf Domain, File "map_e.pos" ];
}
}
}
It is also possible to display local quantities on sections of the mesh, here for example on the plane containing the points (0,0,1), (1,0,1) and (0,1,1):
Print [ v, OnSection { {0,0,1} {1,0,1} {0,1,1} }, File "sec_v.pos" ];
Finally, local quantities can also be interpolated on another mesh than the one on which they have been computed. Six types of grids can be specified for this interpolation: a single point, a set of points evenly distributed on a line, a set of points evenly distributed on a plane, a set of points evenly distributed in a box, a set of points defined by a parametric equation, and a set of elements belonging to a different mesh than the original one:
Print [ e, OnPoint {0,0,1} ];
Print [ e, OnLine { {0,0,1} {1,0,1} } {125} ];
Print [ e, OnPlane { {0,0,1} {1,0,1} {0,1,1} } {125, 75} ];
Print [ e, OnBox { {0,0,1} {1,0,1} {0,1,1} {0,0,2} } {125, 75, 85} ];
Print [ e, OnGrid {$A, $B, 1} { 0:1:1/125, 0:1:1/75, 0 } ];
Print [ e, OnGrid Domain2 ];
Many options can be used to modify the aspect of all these maps, as well as
the default behaviour of the Print commands. See Types for PostOperation, to get the list of all these options. For example, to obtain
a map of the scalar potential at the barycenters of the elements on the
boundary of the region Domain, in a table oriented format appended to
an already existing file out.txt, the operation would be:
Print [ v, OnElementsOf Domain, Depth 0, Skin, Format Table,
File >> "out.txt" ];
Global quantities, which are associated with regions (and not with the
elements of the mesh of these regions), are displayed thanks to the
OnRegion operation. For example, the global potential and charge on
the region SkinDomainC can be displayed with:
PostOperation {
{ Name Val_V_Q; NameOfPostProcessing EleSta_vf ;
Operation {
Print [ V, OnRegion SkinDomainC ];
Print [ Q, OnRegion SkinDomainC ];
}
}
}
Next: File formats, Previous: Short examples, Up: Top [Contents][Index]
This chapter presents complete examples that can be run “as is” with GetDP (see Running GetDP).
Many other ready-to-use examples are available on the website of the ONELAB project: http://onelab.info.
| • Electrostatic problem | ||
| • Magnetostatic problem | ||
| • Magnetodynamic problem |
Next: Magnetostatic problem, Previous: Complete examples, Up: Complete examples [Contents][Index]
Let us first consider a simple electrostatic problem. The formulation used is an electric scalar potential formulation (file EleSta_v.pro, including files Jacobian_Lib.pro and Integration_Lib.pro). It is applied to a microstrip line (file mStrip.pro), whose geometry is defined in the file mStrip.geo (see Gmsh examples). The geometry is two-dimensional and by symmetry only one half of the structure is modeled.
Note that the structure of the following files points out the separation of the data describing the particular problem and the method used to solve it (see Numerical tools as objects), and therefore how it is possible to build black boxes adapted to well defined categories of problems. The files are commented (see Comments) and can be run without any modification.
/* -------------------------------------------------------------------
File "mStrip.pro"
This file defines the problem dependent data structures for the
microstrip problem.
To compute the solution:
getdp mStrip -solve EleSta_v
To compute post-results:
getdp mStrip -pos Map
or getdp mStrip -pos Cut
------------------------------------------------------------------- */
Group {
/* Let's start by defining the interface (i.e. elementary groups)
between the mesh file and GetDP (no mesh object is defined, so
the default mesh will be assumed to be in GMSH format and located
in "mStrip.msh") */
Air = Region[101]; Diel1 = Region[111];
Ground = Region[120]; Line = Region[121];
SurfInf = Region[130];
/* We can then define a global group (used in "EleSta_v.pro",
the file containing the function spaces and formulations) */
DomainCC_Ele = Region[{Air, Diel1}];
}
Function {
/* The relative permittivity (needed in the formulation) is piecewise
defined in elementary groups */
epsr[Air] = 1.;
epsr[Diel1] = 9.8;
}
Constraint {
/* Now, some Dirichlet conditions are defined. The name
'ElectricScalarPotential' refers to the constraint name given in
the function space */
{ Name ElectricScalarPotential; Type Assign;
Case {
{ Region Region[{Ground, SurfInf}]; Value 0.; }
{ Region Line; Value 1.e-3; }
}
}
}
/* The formulation used and its tools, considered as being
in a black box, can now be included */
Include "Jacobian_Lib.pro"
Include "Integration_Lib.pro"
Include "EleSta_v.pro"
/* Finally, we can define some operations to output results */
e = 1.e-7;
PostOperation {
{ Name Map; NameOfPostProcessing EleSta_v;
Operation {
Print [ v, OnElementsOf DomainCC_Ele, File "mStrip_v.pos" ];
Print [ e, OnElementsOf DomainCC_Ele, File "mStrip_e.pos" ];
}
}
{ Name Cut; NameOfPostProcessing EleSta_v;
Operation {
Print [ e, OnLine {{e,e,0}{10.e-3,e,0}} {500}, File "Cut_e" ];
}
}
}
/* -------------------------------------------------------------------
File "EleSta_v.pro"
Electrostatics - Electric scalar potential v formulation
-------------------------------------------------------------------
I N P U T
---------
Global Groups : (Extension '_Ele' is for Electric problem)
-------------
Domain_Ele Whole electric domain (not used)
DomainCC_Ele Nonconducting regions
DomainC_Ele Conducting regions (not used)
Function :
--------
epsr[] Relative permittivity
Constraint :
----------
ElectricScalarPotential Fixed electric scalar potential
(classical boundary condition)
Physical constants :
------------------ */
eps0 = 8.854187818e-12;
Group {
DefineGroup[ Domain_Ele, DomainCC_Ele, DomainC_Ele ];
}
Function {
DefineFunction[ epsr ];
}
FunctionSpace {
{ Name Hgrad_v_Ele; Type Form0;
BasisFunction {
// v = v s , for all nodes
// n n
{ Name sn; NameOfCoef vn; Function BF_Node;
Support DomainCC_Ele; Entity NodesOf[ All ]; }
}
Constraint {
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint ElectricScalarPotential; }
}
}
}
Formulation {
{ Name Electrostatics_v; Type FemEquation;
Quantity {
{ Name v; Type Local; NameOfSpace Hgrad_v_Ele; }
}
Equation {
Galerkin { [ epsr[] * Dof{d v} , {d v} ]; In DomainCC_Ele;
Jacobian Vol; Integration GradGrad; }
}
}
}
Resolution {
{ Name EleSta_v;
System {
{ Name Sys_Ele; NameOfFormulation Electrostatics_v; }
}
Operation {
Generate[Sys_Ele]; Solve[Sys_Ele]; SaveSolution[Sys_Ele];
}
}
}
PostProcessing {
{ Name EleSta_v; NameOfFormulation Electrostatics_v;
Quantity {
{ Name v;
Value {
Local { [ {v} ]; In DomainCC_Ele; Jacobian Vol; }
}
}
{ Name e;
Value {
Local { [ -{d v} ]; In DomainCC_Ele; Jacobian Vol; }
}
}
{ Name d;
Value {
Local { [ -eps0*epsr[] * {d v} ]; In DomainCC_Ele;
Jacobian Vol; }
}
}
}
}
}
/* -------------------------------------------------------------------
File "Jacobian_Lib.pro"
Definition of a jacobian method
-------------------------------------------------------------------
I N P U T
---------
GlobalGroup :
-----------
DomainInf Regions with Spherical Shell Transformation
Parameters :
----------
Val_Rint, Val_Rext Inner and outer radius of the Spherical Shell
of DomainInf
*/
Group {
DefineGroup[ DomainInf ] ;
DefineVariable[ Val_Rint, Val_Rext ] ;
}
Jacobian {
{ Name Vol ;
Case { { Region DomainInf ;
Jacobian VolSphShell {Val_Rint, Val_Rext} ; }
{ Region All ; Jacobian Vol ; }
}
}
}
/* -------------------------------------------------------------------
File "Integration_Lib.pro"
Definition of integration methods
------------------------------------------------------------------- */
Integration {
{ Name GradGrad ;
Case { {Type Gauss ;
Case { { GeoElement Triangle ; NumberOfPoints 4 ; }
{ GeoElement Quadrangle ; NumberOfPoints 4 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 4 ; }
{ GeoElement Hexahedron ; NumberOfPoints 6 ; }
{ GeoElement Prism ; NumberOfPoints 9 ; } }
}
}
}
{ Name CurlCurl ;
Case { {Type Gauss ;
Case { { GeoElement Triangle ; NumberOfPoints 4 ; }
{ GeoElement Quadrangle ; NumberOfPoints 4 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 4 ; }
{ GeoElement Hexahedron ; NumberOfPoints 6 ; }
{ GeoElement Prism ; NumberOfPoints 9 ; } }
}
}
}
}
Next: Magnetodynamic problem, Previous: Electrostatic problem, Up: Complete examples [Contents][Index]
We now consider a magnetostatic problem. The formulation used is a 2D magnetic vector potential formulation (see file MagSta_a_2D.pro). It is applied to a core-inductor system (file CoreSta.pro), whose geometry is defined in theh file Core.geo (see Gmsh examples). The geometry is two-dimensional and, by symmetry, one fourth of the structure is modeled.
The jacobian and integration methods used are the same as for the electrostatic problem presented in Electrostatic problem.
/* -------------------------------------------------------------------
File "CoreSta.pro"
This file defines the problem dependent data structures for the
static core-inductor problem.
To compute the solution:
getdp CoreSta -msh Core.msh -solve MagSta_a_2D
To compute post-results:
getdp CoreSta -msh Core.msh -pos Map_a
------------------------------------------------------------------- */
Group {
Air = Region[ 101 ]; Core = Region[ 102 ];
Ind = Region[ 103 ]; AirInf = Region[ 111 ];
SurfaceGh0 = Region[ 1100 ]; SurfaceGe0 = Region[ 1101 ];
SurfaceGInf = Region[ 1102 ];
Val_Rint = 200.e-3;
Val_Rext = 250.e-3;
DomainCC_Mag = Region[ {Air, AirInf, Core, Ind} ];
DomainC_Mag = Region[ {} ];
DomainS_Mag = Region[ {Ind} ]; // Stranded inductor
DomainInf = Region[ {AirInf} ];
Domain_Mag = Region[ {DomainCC_Mag, DomainC_Mag} ];
}
Function {
mu0 = 4.e-7 * Pi;
murCore = 100.;
nu [ Region[{Air, Ind, AirInf}] ] = 1. / mu0;
nu [ Core ] = 1. / (murCore * mu0);
Sc[ Ind ] = 2.5e-2 * 5.e-2;
}
Constraint {
{ Name MagneticVectorPotential_2D;
Case {
{ Region SurfaceGe0 ; Value 0.; }
{ Region SurfaceGInf; Value 0.; }
}
}
Val_I_1_ = 0.01 * 1000.;
{ Name SourceCurrentDensityZ;
Case {
{ Region Ind; Value Val_I_1_/Sc[]; }
}
}
}
Include "Jacobian_Lib.pro"
Include "Integration_Lib.pro"
Include "MagSta_a_2D.pro"
e = 1.e-5;
p1 = {e,e,0};
p2 = {0.12,e,0};
PostOperation {
{ Name Map_a; NameOfPostProcessing MagSta_a_2D;
Operation {
Print[ az, OnElementsOf Domain_Mag, File "CoreSta_a.pos" ];
Print[ b, OnLine{{List[p1]}{List[p2]}} {1000}, File "k_a" ];
}
}
}
/* -------------------------------------------------------------------
File "MagSta_a_2D.pro"
Magnetostatics - Magnetic vector potential a formulation (2D)
-------------------------------------------------------------------
I N P U T
---------
GlobalGroup : (Extension '_Mag' is for Magnetic problem)
-----------
Domain_Mag Whole magnetic domain
DomainS_Mag Inductor regions (Source)
Function :
--------
nu[] Magnetic reluctivity
Constraint :
----------
MagneticVectorPotential_2D
Fixed magnetic vector potential (2D)
(classical boundary condition)
SourceCurrentDensityZ Fixed source current density (in Z direction)
*/
Group {
DefineGroup[ Domain_Mag, DomainS_Mag ];
}
Function {
DefineFunction[ nu ];
}
FunctionSpace {
// Magnetic vector potential a (b = curl a)
{ Name Hcurl_a_Mag_2D; Type Form1P;
BasisFunction {
// a = a s
// e e
{ Name se; NameOfCoef ae; Function BF_PerpendicularEdge;
Support Domain_Mag; Entity NodesOf[ All ]; }
}
Constraint {
{ NameOfCoef ae; EntityType NodesOf;
NameOfConstraint MagneticVectorPotential_2D; }
}
}
// Source current density js (fully fixed space)
{ Name Hregion_j_Mag_2D; Type Vector;
BasisFunction {
{ Name sr; NameOfCoef jsr; Function BF_RegionZ;
Support DomainS_Mag; Entity DomainS_Mag; }
}
Constraint {
{ NameOfCoef jsr; EntityType Region;
NameOfConstraint SourceCurrentDensityZ; }
}
}
}
Formulation {
{ Name Magnetostatics_a_2D; Type FemEquation;
Quantity {
{ Name a ; Type Local; NameOfSpace Hcurl_a_Mag_2D; }
{ Name js; Type Local; NameOfSpace Hregion_j_Mag_2D; }
}
Equation {
Galerkin { [ nu[] * Dof{d a} , {d a} ]; In Domain_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { [ - Dof{js} , {a} ]; In DomainS_Mag;
Jacobian Vol; Integration CurlCurl; }
}
}
}
Resolution {
{ Name MagSta_a_2D;
System {
{ Name Sys_Mag; NameOfFormulation Magnetostatics_a_2D; }
}
Operation {
Generate[Sys_Mag]; Solve[Sys_Mag]; SaveSolution[Sys_Mag];
}
}
}
PostProcessing {
{ Name MagSta_a_2D; NameOfFormulation Magnetostatics_a_2D;
Quantity {
{ Name a;
Value {
Local { [ {a} ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name az;
Value {
Local { [ CompZ[{a}] ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name b;
Value {
Local { [ {d a} ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name h;
Value {
Local { [ nu[] * {d a} ]; In Domain_Mag; Jacobian Vol; }
}
}
}
}
}
Previous: Magnetostatic problem, Up: Complete examples [Contents][Index]
As a third example we consider a magnetodynamic problem. The formulation is a two-dimensional a-v formulation (see file MagDyn_av_2D.pro, which includes the same jacobian and integration library files as in Electrostatic problem). It is applied to a core-inductor system (defined in file CoreMassive.pro), whose geometry has already been defined in file Core.geo.
/* -------------------------------------------------------------------
File "CoreMassive.pro"
This file defines the problem dependent data structures for the
dynamic core-inductor problem.
To compute the solution:
getdp CoreMassive -msh Core.msh -solve MagDyn_av_2D
To compute post-results:
getdp CoreMassive -msh Core.msh -pos Map_a
getdp CoreMassive -msh Core.msh -pos U_av
------------------------------------------------------------------- */
Group {
Air = Region[ 101 ]; Core = Region[ 102 ];
Ind = Region[ 103 ]; AirInf = Region[ 111 ];
SurfaceGh0 = Region[ 1100 ]; SurfaceGe0 = Region[ 1101 ];
SurfaceGInf = Region[ 1102 ];
Val_Rint = 200.e-3;
Val_Rext = 250.e-3;
DomainCC_Mag = Region[ {Air, AirInf} ];
DomainC_Mag = Region[ {Ind, Core} ]; // Massive inductor + conducting core
DomainB_Mag = Region[ {} ];
DomainS_Mag = Region[ {} ];
DomainInf = Region[ {AirInf} ];
Domain_Mag = Region[ {DomainCC_Mag, DomainC_Mag} ];
}
Function {
mu0 = 4.e-7 * Pi;
murCore = 100.;
nu [ #{Air, Ind, AirInf} ] = 1. / mu0;
nu [ Core ] = 1. / (murCore * mu0);
sigma [ Ind ] = 5.9e7;
sigma [ Core ] = 2.5e7;
Freq = 1.;
}
Constraint {
{ Name MagneticVectorPotential_2D;
Case {
{ Region SurfaceGe0 ; Value 0.; }
{ Region SurfaceGInf; Value 0.; }
}
}
{ Name SourceCurrentDensityZ;
Case {
}
}
Val_I_ = 0.01 * 1000.;
{ Name Current_2D;
Case {
{ Region Ind; Value Val_I_; }
}
}
{ Name Voltage_2D;
Case {
{ Region Core; Value 0.; }
}
}
}
Include "Jacobian_Lib.pro"
Include "Integration_Lib.pro"
Include "MagDyn_av_2D.pro"
PostOperation {
{ Name Map_a; NameOfPostProcessing MagDyn_av_2D;
Operation {
Print[ az, OnElementsOf Domain_Mag, File "Core_m_a.pos" ];
Print[ j, OnElementsOf Domain_Mag, File "Core_m_j.pos" ];
}
}
{ Name U_av; NameOfPostProcessing MagDyn_av_2D;
Operation {
Print[ U, OnRegion Ind ];
Print[ I, OnRegion Ind ];
}
}
}
/* -------------------------------------------------------------------
File "MagDyn_av_2D.pro"
Magnetodynamics - Magnetic vector potential and electric scalar
potential a-v formulation (2D)
-------------------------------------------------------------------
I N P U T
---------
GlobalGroup : (Extension '_Mag' is for Magnetic problem)
-----------
Domain_Mag Whole magnetic domain
DomainCC_Mag Nonconducting regions (not used)
DomainC_Mag Conducting regions
DomainS_Mag Inductor regions (Source)
DomainV_Mag All regions in movement (for speed term)
Function :
--------
nu[] Magnetic reluctivity
sigma[] Electric conductivity
Velocity[] Velocity of regions
Constraint :
----------
MagneticVectorPotential_2D
Fixed magnetic vector potential (2D)
(classical boundary condition)
SourceCurrentDensityZ Fixed source current density (in Z direction)
Voltage_2D Fixed voltage
Current_2D Fixed Current
Parameters :
----------
Freq Frequency (Hz)
Parameters for time loop with theta scheme :
Mag_Time0, Mag_TimeMax, Mag_DTime
Initial time, Maximum time, Time step (s)
Mag_Theta Theta (e.g. 1. : Implicit Euler,
0.5 : Cranck Nicholson)
*/
Group {
DefineGroup[ Domain_Mag, DomainCC_Mag, DomainC_Mag,
DomainS_Mag, DomainV_Mag ];
}
Function {
DefineFunction[ nu, sigma ];
DefineFunction[ Velocity ];
DefineVariable[ Freq ];
DefineVariable[ Mag_Time0, Mag_TimeMax, Mag_DTime, Mag_Theta ];
}
FunctionSpace {
// Magnetic vector potential a (b = curl a)
{ Name Hcurl_a_Mag_2D; Type Form1P;
BasisFunction {
// a = a s
// e e
{ Name se; NameOfCoef ae; Function BF_PerpendicularEdge;
Support Domain_Mag; Entity NodesOf[ All ]; }
}
Constraint {
{ NameOfCoef ae; EntityType NodesOf;
NameOfConstraint MagneticVectorPotential_2D; }
}
}
// Gradient of Electric scalar potential (2D)
{ Name Hregion_u_Mag_2D; Type Form1P;
BasisFunction {
{ Name sr; NameOfCoef ur; Function BF_RegionZ;
Support DomainC_Mag; Entity DomainC_Mag; }
}
GlobalQuantity {
{ Name U; Type AliasOf ; NameOfCoef ur; }
{ Name I; Type AssociatedWith; NameOfCoef ur; }
}
Constraint {
{ NameOfCoef U; EntityType Region;
NameOfConstraint Voltage_2D; }
{ NameOfCoef I; EntityType Region;
NameOfConstraint Current_2D; }
}
}
// Source current density js (fully fixed space)
{ Name Hregion_j_Mag_2D; Type Vector;
BasisFunction {
{ Name sr; NameOfCoef jsr; Function BF_RegionZ;
Support DomainS_Mag; Entity DomainS_Mag; }
}
Constraint {
{ NameOfCoef jsr; EntityType Region;
NameOfConstraint SourceCurrentDensityZ; }
}
}
}
Formulation {
{ Name Magnetodynamics_av_2D; Type FemEquation;
Quantity {
{ Name a ; Type Local ; NameOfSpace Hcurl_a_Mag_2D; }
{ Name ur; Type Local ; NameOfSpace Hregion_u_Mag_2D; }
{ Name I ; Type Global; NameOfSpace Hregion_u_Mag_2D [I]; }
{ Name U ; Type Global; NameOfSpace Hregion_u_Mag_2D [U]; }
{ Name js; Type Local ; NameOfSpace Hregion_j_Mag_2D; }
}
Equation {
Galerkin { [ nu[] * Dof{d a} , {d a} ]; In Domain_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { DtDof [ sigma[] * Dof{a} , {a} ]; In DomainC_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { [ sigma[] * Dof{ur} , {a} ]; In DomainC_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { [ - sigma[] * (Velocity[] *^ Dof{d a}) , {a} ];
In DomainV_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { [ - Dof{js} , {a} ]; In DomainS_Mag;
Jacobian Vol;
Integration CurlCurl; }
Galerkin { DtDof [ sigma[] * Dof{a} , {ur} ]; In DomainC_Mag;
Jacobian Vol; Integration CurlCurl; }
Galerkin { [ sigma[] * Dof{ur} , {ur} ]; In DomainC_Mag;
Jacobian Vol; Integration CurlCurl; }
GlobalTerm { [ Dof{I} , {U} ]; In DomainC_Mag; }
}
}
}
Resolution {
{ Name MagDyn_av_2D;
System {
{ Name Sys_Mag; NameOfFormulation Magnetodynamics_av_2D;
Type ComplexValue; Frequency Freq; }
}
Operation {
Generate[Sys_Mag]; Solve[Sys_Mag]; SaveSolution[Sys_Mag];
}
}
{ Name MagDyn_t_av_2D;
System {
{ Name Sys_Mag; NameOfFormulation Magnetodynamics_av_2D; }
}
Operation {
InitSolution[Sys_Mag]; SaveSolution[Sys_Mag];
TimeLoopTheta[Mag_Time0, Mag_TimeMax, Mag_DTime, Mag_Theta] {
Generate[Sys_Mag]; Solve[Sys_Mag]; SaveSolution[Sys_Mag];
}
}
}
}
PostProcessing {
{ Name MagDyn_av_2D; NameOfFormulation Magnetodynamics_av_2D;
Quantity {
{ Name a;
Value {
Local { [ {a} ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name az;
Value {
Local { [ CompZ[{a}] ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name b;
Value {
Local { [ {d a} ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name h;
Value {
Local { [ nu[] * {d a} ]; In Domain_Mag; Jacobian Vol; }
}
}
{ Name j;
Value {
Local { [ - sigma[]*(Dt[{a}]+{ur}) ]; In DomainC_Mag;
Jacobian Vol; }
}
}
{ Name jz;
Value {
Local { [ - sigma[]*CompZ[Dt[{a}]+{ur}] ]; In DomainC_Mag;
Jacobian Vol; }
}
}
{ Name roj2;
Value {
Local { [ sigma[]*SquNorm[Dt[{a}]+{ur}] ]; In DomainC_Mag;
Jacobian Vol; }
}
}
{ Name U; Value { Local { [ {U} ]; In DomainC_Mag; } } }
{ Name I; Value { Local { [ {I} ]; In DomainC_Mag; } } }
}
}
}
Next: Gmsh examples, Previous: Complete examples, Up: Top [Contents][Index]
This chapter describes the file formats that cannot be modified by the user. The format of the problem definition structure is explained in Objects, and Types for objects. The format of the post-processing files is explained in Types for PostOperation.
| • Input file format | ||
| • Output file format |
Next: Output file format, Previous: File formats, Up: File formats [Contents][Index]
The native mesh format read by GetDP is the mesh file format produced by Gmsh (http://gmsh.info). In its “version 1” incarnation, an ‘msh’ file is divided into two sections, defining the nodes and the elements in the mesh.
$NOD number-of-nodes node-number x-coord y-coord z-coord … $ENDNOD $ELM number-of-elements elm-number elm-type elm-region unused number-of-nodes node-numbers … $ENDELM
All the syntactic variables stand for integers except x-coord, y-coord and z-coord which stand for floating point values. The elm-type value defines the geometrical type for the element:
elm-type:
1Line (2 nodes, 1 edge).
2Triangle (3 nodes, 3 edges).
3Quadrangle (4 nodes, 4 edges).
4Tetrahedron (4 nodes, 6 edges, 4 facets).
5Hexahedron (8 nodes, 12 edges, 6 facets).
6Prism (6 nodes, 9 edges, 5 facets).
7Pyramid (5 nodes, 8 edges, 5 facets).
15Point (1 node).
GetDP can also read more recent versions of the ‘msh’ format (2.0 and above), as well as binary meshes. See the Gmsh documentation for more information about these formats.
Previous: Input file format, Up: File formats [Contents][Index]
| • File pre | ||
| • File res |
Next: File res, Previous: Output file format, Up: Output file format [Contents][Index]
The .pre file is generated by the pre-processing stage. It contains all the information about the degrees of freedom to be considered during the processing stage for a given resolution (i.e., unknowns, fixed values, initial values, etc.).
$Resolution /* 'resolution-id' */ main-resolution-number number-of-dofdata $EndResolution $DofData /* #dofdata-number */ resolution-number system-number number-of-function-spaces function-space-number … number-of-time-functions time-function-number … number-of-partitions partition-index … number-of-any-dof number-of-dof dof-basis-function-number dof-entity dof-harmonic dof-type dof-data … $EndDofData …
with
dof-data:
equation-number nnz
(dof-type: 1; unknown) |
dof-value dof-time-function-number
(dof-type: 2; fixed value) |
dof-associate-dof-number dof-value dof-time-function-number
(dof-type: 3; associated degree of freedom) |
equation-number dof-value
(dof-type: 5; initial value for an unknown)
Notes:
$DofData field for each system of equations considered in
the resolution (including those considered in pre-resolutions).
$DofData field is determined by the order
of this field in the .pre file.
Previous: File pre, Up: Output file format [Contents][Index]
The .res file is generated by the processing stage. It contains the solution of the problem (or a part of it in case of program interruption).
$ResFormat /* GetDP vgetdp-version-number, string-for-format */ 1.1 file-res-format $EndResFormat $Solution /* DofData #dofdata-number */ dofdata-number time-value time-imag-value time-step-number solution-value … $EndSolution …
Notes:
$Solution field contains the solution associated with a
$DofData field.
$Solution field for each time step, of which the time is
time-value (0 for non time dependent or non modal analyses) and the
imaginary time is time-imag-value (0 for non time dependent or non
modal analyses).
$Solution field follows
the numbering of the equations given in the .pre file
(one floating point value for each degree of freedom).
Next: Compiling the source code, Previous: File formats, Up: Top [Contents][Index]
Gmsh is a three-dimensional finite element mesh generator with simple CAD and post-processing capabilities that can be used as a graphical front-end for GetDP. Gmsh can be downloaded from http://gmsh.info.
This appendix reproduces verbatim the input files needed by Gmsh to produce the mesh files mStrip.msh and Core.msh used in the examples of Complete examples.
/* -------------------------------------------------------------------
File "mStrip.geo"
This file is the geometrical description used by GMSH to produce
the file "mStrip.msh".
------------------------------------------------------------------- */
/* Definition of some parameters for geometrical dimensions, i.e.
h (height of 'Diel1'), w (width of 'Line'), t (thickness of 'Line')
xBox (width of the air box) and yBox (height of the air box) */
h = 1.e-3 ; w = 4.72e-3 ; t = 0.035e-3 ;
xBox = w/2. * 6. ; yBox = h * 12. ;
/* Definition of parameters for local mesh dimensions */
s = 1. ;
p0 = h / 10. * s ;
pLine0 = w/2. / 10. * s ; pLine1 = w/2. / 50. * s ;
pxBox = xBox / 10. * s ; pyBox = yBox / 8. * s ;
/* Definition of gemetrical points */
Point(1) = { 0 , 0, 0, p0} ;
Point(2) = { xBox, 0, 0, pxBox} ;
Point(3) = { xBox, h, 0, pxBox} ;
Point(4) = { 0 , h, 0, pLine0} ;
Point(5) = { w/2., h, 0, pLine1} ;
Point(6) = { 0 , h+t, 0, pLine0} ;
Point(7) = { w/2., h+t, 0, pLine1} ;
Point(8) = { 0 , yBox, 0, pyBox} ;
Point(9) = { xBox, yBox, 0, pyBox} ;
/* Definition of gemetrical lines */
Line(1) = {1,2}; Line(2) = {2,3}; Line(3) = {3,9};
Line(4) = {9,8}; Line(5) = {8,6}; Line(7) = {4,1};
Line(8) = {5,3}; Line(9) = {4,5}; Line(10) = {6,7};
Line(11) = {5,7};
/* Definition of geometrical surfaces */
Line Loop(12) = {8,-2,-1,-7,9}; Plane Surface(13) = {12};
Line Loop(14) = {10,-11,8,3,4,5}; Plane Surface(15) = {14};
/* Definition of Physical entities (surfaces, lines). The Physical
entities tell GMSH the elements and their associated region numbers
to save in the file 'mStrip.msh'. For example, the Region
111 is made of elements of surface 13, while the Region 121 is
made of elements of lines 9, 10 and 11 */
Physical Surface (101) = {15} ; /* Air */
Physical Surface (111) = {13} ; /* Diel1 */
Physical Line (120) = {1} ; /* Ground */
Physical Line (121) = {9,10,11} ; /* Line */
Physical Line (130) = {2,3,4} ; /* SurfInf */
/* -------------------------------------------------------------------
File "Core.geo"
This file is the geometrical description used by GMSH to produce
the file "Core.msh".
------------------------------------------------------------------- */
dxCore = 50.e-3; dyCore = 100.e-3;
xInd = 75.e-3; dxInd = 25.e-3; dyInd = 50.e-3;
rInt = 200.e-3; rExt = 250.e-3;
s = 1.;
p0 = 12.e-3 *s;
pCorex = 4.e-3 *s; pCorey0 = 8.e-3 *s; pCorey = 4.e-3 *s;
pIndx = 5.e-3 *s; pIndy = 5.e-3 *s;
pInt = 12.5e-3*s; pExt = 12.5e-3*s;
Point(1) = {0,0,0,p0};
Point(2) = {dxCore,0,0,pCorex};
Point(3) = {dxCore,dyCore,0,pCorey};
Point(4) = {0,dyCore,0,pCorey0};
Point(5) = {xInd,0,0,pIndx};
Point(6) = {xInd+dxInd,0,0,pIndx};
Point(7) = {xInd+dxInd,dyInd,0,pIndy};
Point(8) = {xInd,dyInd,0,pIndy};
Point(9) = {rInt,0,0,pInt};
Point(10) = {rExt,0,0,pExt};
Point(11) = {0,rInt,0,pInt};
Point(12) = {0,rExt,0,pExt};
Line(1) = {1,2}; Line(2) = {2,5}; Line(3) = {5,6};
Line(4) = {6,9}; Line(5) = {9,10}; Line(6) = {1,4};
Line(7) = {4,11}; Line(8) = {11,12}; Line(9) = {2,3};
Line(10) = {3,4}; Line(11) = {6,7}; Line(12) = {7,8};
Line(13) = {8,5};
Circle(14) = {9,1,11}; Circle(15) = {10,1,12};
Line Loop(16) = {-6,1,9,10}; Plane Surface(17) = {16};
Line Loop(18) = {11,12,13,3}; Plane Surface(19) = {18};
Line Loop(20) = {7,-14,-4,11,12,13,-2,9,10}; Plane Surface(21) = {20};
Line Loop(22) = {8,-15,-5,14}; Plane Surface(23) = {22};
Physical Surface(101) = {21}; /* Air */
Physical Surface(102) = {17}; /* Core */
Physical Surface(103) = {19}; /* Ind */
Physical Surface(111) = {23}; /* AirInf */
Physical Line(1000) = {1,2}; /* Cut */
Physical Line(1001) = {2}; /* CutAir */
Physical Line(202) = {9,10}; /* SkinCore */
Physical Line(203) = {11,12,13}; /* SkinInd */
Physical Line(1100) = {1,2,3,4,5}; /* SurfaceGh0 */
Physical Line(1101) = {6,7,8}; /* SurfaceGe0 */
Physical Line(1102) = {15}; /* SurfaceGInf */
Next: Frequently asked questions, Previous: Gmsh examples, Up: Top [Contents][Index]
Stable releases and source snapshots are available from http://getdp.info/src/. You can also access the Git repository directly:
git pull
Once you have the source code, you need to run CMake to configure your build (see the README.txt file in the top-level source directory for detailed information on how to run CMake).
Each build can be configured using a series of options, to selectively enable optional modules or features. Here is the list of CMake options:
ENABLE_ARPACK
Enable Arpack eigensolver (requires Fortran) (default: ON)
ENABLE_BLAS_LAPACK
Enable BLAS/Lapack for linear algebra (e.g. for Arpack) (default: ON)
ENABLE_BUILD_LIB
Enable ’lib’ target for building static GetDP library (default: OFF)
ENABLE_BUILD_SHARED
Enable ’shared’ target for building shared GetDP library (default: OFF)
ENABLE_BUILD_DYNAMIC
Enable dynamic GetDP executable (linked with shared lib) (default: OFF)
ENABLE_BUILD_ANDROID
Enable Android NDK library target (experimental) (default: OFF)
ENABLE_BUILD_IOS
Enable iOS (ARM) library target (experimental) (default: OFF)
ENABLE_FORTRAN
Enable Fortran (needed for Arpack/Sparskit/Zitsol & Bessel) (default: ON)
ENABLE_GMSH
Enable Gmsh functions (for field interpolation) (default: ON)
ENABLE_GSL
Enable GSL functions (for some built-in functions) (default: ON)
ENABLE_KERNEL
Enable kernel (required for actual computations) (default: ON)
ENABLE_MMA
Enable MMA optimizer (default: ON)
ENABLE_MPI
Enable MPI parallelization (with PETSc/SLEPc) (default: OFF)
ENABLE_MULTIHARMONIC
Enable multi-harmonic support (default: OFF)
ENABLE_NR
Enable NR functions (if GSL is unavailable) (default: ON)
ENABLE_NX
Enable proprietary NX extension (default: OFF)
ENABLE_OCTAVE
Enable Octave functions (default: OFF)
ENABLE_OPENMP
Enable OpenMP parallelization of some functions (experimental) (default: OFF)
ENABLE_PETSC
Enable PETSc linear solver (default: ON)
ENABLE_PRIVATE_API
Enable private API (default: OFF)
ENABLE_PYTHON
Enable Python functions (default: ON)
ENABLE_SLEPC
Enable SLEPc eigensolver (default: ON)
ENABLE_SMALLFEM
Enable experimental SmallFem assembler (default: OFF)
ENABLE_SPARSKIT
Enable Sparskit solver instead of PETSc (requires Fortran) (default: ON)
ENABLE_SYSTEM_CONTRIB
Use system versions of contrib libraries, when possible (default: OFF)
ENABLE_PEWE
Enable PeWe exact solutions (requires Fortran) (default: ON)
ENABLE_WRAP_PYTHON
Build Python wrappers (default: OFF)
ENABLE_ZITSOL
Enable Zitsol solvers (requires PETSc and Fortran) (default: OFF)
Next: Tips and tricks, Previous: Compiling the source code, Up: Top [Contents][Index]
| • The basics | ||
| • Installation | ||
| • Usage |
Next: Installation, Previous: Frequently asked questions, Up: Frequently asked questions [Contents][Index]
GetDP is a scientific software environment for the numerical solution of integro-differential equations, open to the coupling of physical problems (electromagnetic, thermal, mechanical, etc) as well as of numerical methods (finite element method, integral methods, etc). It can deal with such problems of various dimensions (1D, 2D, 2D axisymmetric or 3D) and time states (static, transient or harmonic). The main feature of GetDP is the closeness between the organization of data defining discrete problems (written by the user in ASCII data files) and the symbolic mathematical expressions of these problems.
GetDP is distributed under the terms of the GNU General Public License. See License for more information.
It’s an acronym for a “General environment for the treatment of Discrete Problems”.
http://getdp.info is the primary location to obtain information about GetDP. There you will for example find the complete reference manual and the bug tracking database.
Next: Usage, Previous: The basics, Up: Frequently asked questions [Contents][Index]
Gmsh runs on Windows, MacOS X, Linux and most Unix variants.
You need a C++ and a Fortran compiler as well as the GSL (version 1.2 or higher; freely available from http://sources.redhat.com/gsl).
You need cmake (http://www.cmake.org) and a C++ compiler (and a Fortran compiler depending on the modules/solvers you want to compile). See Compiling the source code and the README.txt file in the top-level source directory for more information.
Try ldd getdp (or otool -L getdp on MacOS X) to check if
all the required shared libraries are installed on your system. If not,
install them. If it still doesn’t work, recompile GetDP from the
sources.
Previous: Installation, Up: Frequently asked questions [Contents][Index]
The only meshing format accepted by this version of GetDP is the ‘msh’ format created by Gmsh http://gmsh.info. This format being very simple (see the Gmsh reference manual for more details), it should be straightforward to write a converter from your mesh format to the ‘msh’ format.
You can specify a format in all post-processing operations. Available
formats include Table, SimpleTable, TimeTable and
Gmsh. Table, SimpleTable and TimeTable
output lists of numbers easily readable by Excel/gnuplot/Caleida
Graph/etc. Gmsh outputs post-processing views directly loadable
by Gmsh.
It depends on which linear solver toolkit was enabled when GetDP was compiled (PETSc or Sparskit).
With PETSc-based linear solvers you can either specify options on the
command line (e.g. with -ksp_type gmres -pc_type ilu), through a
specific option file (with -solver file), through the
.petscrc file located in your home directly, or directly in the
Resolution field using the SetGlobalSolverOptions[]
command.
With Sparskit-based linear solvers can either specify options directly
on command line (e.g. with -Nb_Fill 200), specify an option file
explicitly (with -solver file), or edit the solver.par
file in the current working directory. If no solver.par file
exists in the current directory, GetDP will give create it the next time
you perform a linear system solution.
Next: Version history, Previous: Frequently asked questions, Up: Top [Contents][Index]
.emacs file: (setq auto-mode-alist (append '(("\\.pro$"
. c++-mode)) auto-mode-alist)).
All as soon as possible in the definition of topological
entities used as Entity of BasisFunctions.
This will prevent GetDP from constructing unnecessary lists of entities.
Next: Copyright and credits, Previous: Tips and tricks, Up: Top [Contents][Index]
3.5.0 (May 13, 2022): generalized Trace operator on non-conforming meshes; new
Errf function; source code reorganization.
3.4.0 (September 23, 2021): new Min and Max functions on constants (at parse
time); fixed regression in trees of edges in 2D; added support for non-ASCII
paths on command line on Windows; GetDP now requires C++11 and CMake 3.3; small
bug fixes.
3.3.0 (December 21, 2019): improved support for curved elements; added support
for auto-similar trees of edges (e.g. for sliding surfaces in 3D); update for
latest Gmsh version.
3.2.0 (July 1, 2019): improved node and edge link constraints search using
rtree; added support for BF_Edge basis functions on curved elements; small
fixes.
3.1.0 (April 19, 2019): added support for high-order (curved) Lagrange elements
(P2, P3 and P4); added support for latest Gmsh version; code refactoring.
3.0.4 (December 9, 2018): allow general groups in Jacobian definitions; fixed
string parser regression.
3.0.3 (October 18, 2018): new AtGaussPoint PostOperation option; bug fixes.
3.0.2 (September 10, 2018): small compilation fixes.
3.0.1 (September 7, 2018): small bug fixes.
3.0.0 (August 22, 2018): new extrapolation (see SetExtrapolationOrder) in
time-domain resolutions; new string macros; added support for Gmsh MSH4 file
format; new file handling operations and ElementTable format in PostOperation;
added support for curved (2nd order) simplices; enhanced communication of
post-processing data with ONELAB; many new functions (Atanh, JnSph, YnSph,
ValueFromTable, ListFromServer, GroupExists, ...); various small bug fixes.
2.11.3 (November 5, 2017): new 'Eig' operator for general eigenvalue problems
(polynomial, rational); small improvements and bug fixes.
2.11.2 (June 23, 2017): minor build system changes.
2.11.1 (May 13, 2017): small bug fixes and improvements.
2.11.0 (January 3, 2017): small improvements (complex math functions, mutual
terms, one side of, get/save runtime variables) and bug fixes.
2.10.0 (October 9, 2016): ONELAB 1.3 with usability and performance
improvements.
2.9.2 (August 21, 2016): small bug fixes.
2.9.1 (August 18, 2016): small improvements (CopySolution[], -cpu) and bug
fixes.
2.9.0 (July 11, 2016): new ONELAB 1.2 protocol with native support for lists;
simple C++ and Python API for exchanging (lists of) numbers and strings;
extended .pro language for the construction of extensible problem definitions
("Append"); new VolCylShell transformation; new functions (Min, Max, SetDTime,
...); small fixes.
2.8.0 (March 5, 2016): new Parse[], {Set,Get}{Number,String}[] and
OnPositiveSideOf commands; added support for lists of strings; various
improvements and bug fixes for better interactive use with ONELAB.
2.7.0 (November 7, 2015): new Else/ElseIf commands; new timing and memory
reporting functions.
2.6.1 (July 30, 2015): enhanced Print[] command; minor fixes.
2.6.0 (July 21, 2015): new ability to define and use Macros in .pro files; new
run-time variables (act as registers, but with user-defined names starting with
'$') and run-time ONELAB Get/Set functions; new Append*ToFileName PostOperation
options; new GetResdidual and associated operations; fixes and extended format
support in MSH file reader; fixed UpdateConstraint for complex-simulated-real
and multi-harmonic calculations.
2.5.1 (April 18, 2015): enhanced Python[] and DefineFunction[].
2.5.0 (March 12, 2015): added option to embed Octave and Python interpreters;
extended "Field" functions with gradient; extended string and list handling
functions; new resolution and postprocessing functions (RenameFile, While, ...);
extended EigenSolve with eigenvalue filter and high order polynomial EV
problems; small bug fixes.
2.4.4 (July 9, 2014): better stability, updated onelab API version and inline
parameter definitions, fixed UpdateConstraint in harmonic case, improved
performance of multi-harmonic assembly, fixed memory leak in parallel MPI
version, improved EigenSolve (quadratic EVP with SLEPC, EVP on real matrices),
new CosineTransform, MPI_Printf, SendMergeFileRequest parser commands, small
improvements and bug fixes.
2.4.3 (February 7, 2014): new mandatory 'Name' attribute to define onelab
variables in DefineConstant[] & co; minor bug fixes.
2.4.2 (Septembre 27, 2013): fixed function arguments in nested expressions;
minor improvements.
2.4.1 (July 16, 2013): minor improvements and bug fixes.
2.4.0 (July 9, 2013): new two-step Init constraints; faster network computation
(with new -cache); improved Update operation; better cpu/memory reporting; new
-setnumber, -setstring and -gmshread command line options; accept unicode file
paths on Windows; small bug fixes.
2.3.1 (May 11, 2013): updated onelab; small bug fixes.
2.3.0 (March 9, 2013): moved build system from autoconf to cmake; new family of
Field functions to use data imported from Gmsh; improved list handling; general
code cleanup.
2.2.1 (July 15, 2012): cleaned up nonlinear convergence tests and integrated
experimental adaptive time loop code; small bug fixes.
2.2.0 (June 19, 2012): new solver interface based on ONELAB; parallel SLEPC
eigensolvers; cleaned up syntax for groups, moving band and global basis
functions; new Field[] functions to interpolate post-processing datasets from
Gmsh; fixed bug in Sur/Lin transformation of 2 forms; fixed bug for periodic
constraints on high-order edge elements.
2.1.1 (April 12, 2011): default direct solver using MUMPS.
2.1.0 (October 24, 2010): parallel resolution using PETSc solvers; new Gmsh2
output format; new experimental SLEPc-based eigensolvers; various bug and
performance fixes (missing face basis functions, slow PETSc assembly with global
quantities, ...)
2.0.0 (March 16, 2010): general code cleanup (separated interface from kernel
code; removed various undocumented, unstable and otherwise experimental
features; moved to C++); updated input file formats; default solvers are now
based on PETSc; small bug fixes (binary .res read, Newmark -restart).
1.2.1 (March 18, 2006): Small fixes.
1.2.0 (March 10, 2006): Windows versions do not depend on Cygwin anymore; major
parser cleanup (loops & co).
1.1.2 (September 3, 2005): Small fixes.
1.1.0 (August 21, 2005): New eigensolver based on Arpack (EigenSolve);
generalized old Lanczos solver to work with GSL+lapack; reworked PETSc
interface, which now requires PETSc 2.3; documented many previously undocumented
features (loops, conditionals, strings, link constraints, etc.); various
improvements and bug fixes.
1.0.1 (February 6, 2005): Small fixes.
1.0.0 (April 24, 2004): New license (GNU GPL); added support for latest Gmsh
mesh file format; more code cleanups.
0.91: Merged moving band and multi-harmonic code; new loops and conditionals in
the parser; removed old readline code (just use GNU readline if available);
upgraded to latest Gmsh post-processing format; various small enhancements and
bug fixes.
0.89 (March 26, 2003): Code cleanup.
0.88: Integrated FMM code.
0.87: Fixed major performance problem on Windows (matrix assembly and
post-processing can be up to 3-4 times faster with 0.87 compared to 0.86,
bringing performance much closer to Unix versions); fixed stack overflow on Mac
OS X; Re-introduced face basis functions mistakenly removed in 0.86; fixed
post-processing bug with pyramidal basis functions; new build system based on
autoconf.
0.86 (January 25, 2003): Updated Gmsh output format; many small bug fixes.
0.85 (January 21, 2002): Upgraded communication interface with Gmsh; new
ChangeOfValues option in PostOperation; many internal changes.
0.84 (September 6, 2001): New ChangeOfCoordinate option in PostOperation; fixed
crash in InterpolationAkima; improved interactive postprocessing (-ipos);
changed syntax of parametric OnGrid ($S, $T -> $A, $B, $C); corrected Skin for
non simplicial meshes; fixed floating point exception in diagonal matrix
scaling; many other small fixes and cleanups.
0.83: Fixed bugs in SaveSolutions[] and InitSolution[]; fixed corrupted binary
post-processing files in the harmonic case for the Gmsh format; output files are
now created relatively to the input file directory; made solver options
available on the command line; added optional matrix scaling and changed default
parameter file name to 'solver.par' (Warning: please check the scaling
definition in your old SOLVER.PAR files); generalized syntax for lists
(start:[incr]end -> start:end:incr); updated reference guide; added a new short
presentation on the web site; OnCut -> OnSection; new functional syntax for
resolution operations (e.g. Generate X -> Generate[X]); many other small fixes
and cleanups.
0.82: Added communication socket for interactive use with Gmsh; corrected
(again) memory problem (leak + seg. fault) in time stepping schemes; corrected
bug in Update[].
0.81: Generalization of transformation jacobians (spherical and rectangular,
with optional parameters); changed handling of missing command line arguments;
enhanced Print OnCut; fixed memory leak for time domain analysis of coupled
problems; -name option; fixed seg. fault in ILUK.
0.80: Fixed computation of time derivatives on first time step (in
post-processing); added tolerance in transformation jacobians; fixed parsing of
DOS files (carriage return problems); automatic memory reallocation in
ILUD/ILUK.
0.79: Various bug fixes (mainly for the post-processing of intergal quantities);
automatic treatment of degenerated cases in axisymmetrical problems.
0.78: Various bug fixes.
0.77: Changed syntax for PostOperations (Plot suppressed in favour of Print;
Plot OnRegion becomes Print OnElementsOf); changed table oriented
post-processing formats; new binary formats; new error diagnostics.
0.76: Reorganized high order shape functions; optimization of the
post-processing (faster and less bloated); lots of internal cleanups.
0.74: High order shape functions; lots of small bug fixes.
0.73: Eigen value problems (Lanczos); minor corrections.
0.7: constraint syntax; fourier transform; unary minus correction; complex
integral quantity correction; separate iteration matrix generation.
0.6: Second order time derivatives; Newton nonlinear scheme; Newmark time
stepping scheme; global quantity syntax; interactive post-processing; tensors;
integral quantities; post-processing facilities.
0.3: First distributed version.
Next: License, Previous: Version history, Up: Top [Contents][Index]
GetDP is copyright (C) 1997-2022
Patrick Dular
and
Christophe Geuzaine
<cgeuzaine at uliege.be>
University of Liege
Major code contributions to GetDP have been provided by Johan Gyselinck, Ruth
Sabariego, Michael Asam, Bertrand Thierry, Francois Henrotte, Guillaume
Dem\'esy. Other code contributors include: David Colignon, Tuan Ledinh, Patrick
Lefevre, Andre Nicolet, Jean-Francois Remacle, Timo Tarhasaari, Christophe
Trophime, Marc Ume and Peter Binde. See the source code for more details.
Thanks to the following folks who have contributed by providing fresh ideas on
theoretical or programming topics, who have sent patches, requests for changes
or improvements, or who gave us access to exotic machines for testing GetDP:
Olivier Adam, Alejandro Angulo, Geoffrey Deliege, Mark Evans, Philippe Geuzaine,
Eric Godard, Sebastien Guenneau, Daniel Kedzierski, Samuel Kvasnica, Benoit
Meys, Uwe Pahner, Georgia Psoni, Robert Struijs, Ahmed Rassili, Thierry
Scordilis, Herve Tortel, Jose Geraldo A. Brito Neto, Matthias Fenner, Daryl Van
Vorst.
The AVL tree code (src/common/avl.*) is copyright (C) 1988-1993, 1995 The Regents
of the University of California. Permission to use, copy, modify, and distribute
this software and its documentation for any purpose and without fee is hereby
granted, provided that the above copyright notice appear in all copies and that
both that copyright notice and this permission notice appear in supporting
documentation, and that the name of the University of California not be used in
advertising or publicity pertaining to distribution of the software without
specific, written prior permission. The University of California makes no
representations about the suitability of this software for any purpose. It is
provided "as is" without express or implied warranty.
The KissFFT code (src/numeric/kissfft.hh) is copyright (c) 2003-2010 Mark
Borgerding. Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met: *
Redistributions of source code must retain the above copyright notice, this list
of conditions and the following disclaimer. * Redistributions in binary form
must reproduce the above copyright notice, this list of conditions and the
following disclaimer in the documentation and/or other materials provided with
the distribution. * Neither the author nor the names of any contributors may be
used to endorse or promote products derived from this software without specific
prior written permission. THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND
CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A
PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR
CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY,
OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING
IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY
OF SUCH DAMAGE.
The picojson code (src/common/picojson.h) is Copyright 2009-2010 Cybozu Labs,
Inc., Copyright 2011-2014 Kazuho Oku, All rights reserved. Redistribution and
use in source and binary forms, with or without modification, are permitted
provided that the following conditions are met: 1. Redistributions of source
code must retain the above copyright notice, this list of conditions and the
following disclaimer. 2. Redistributions in binary form must reproduce the above
copyright notice, this list of conditions and the following disclaimer in the
documentation and/or other materials provided with the distribution. THIS
SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY
EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED
WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR
ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES
(INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES;
LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON
ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT
(INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
This version of GetDP may contain code (in the contrib/Arpack subdirectory)
written by Danny Sorensen, Richard Lehoucq, Chao Yang and Kristi Maschhoff from
the Dept. of Computational & Applied Mathematics at Rice University, Houston,
Texas, USA. See http://www.caam.rice.edu/software/ARPACK/ for more info.
This version of GetDP may contain code (in the contrib/Sparskit subdirectory)
copyright (C) 1990 Yousef Saad: check the configuration options.
Next: Concept index, Previous: Copyright and credits, Up: Top [Contents][Index]
GetDP is provided under the terms of the GNU General Public License
(GPL), Version 2 or later.
GNU GENERAL PUBLIC LICENSE
Version 2, June 1991
Copyright (C) 1989, 1991 Free Software Foundation, Inc.
51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
Everyone is permitted to copy and distribute verbatim copies
of this license document, but changing it is not allowed.
Preamble
The licenses for most software are designed to take away your
freedom to share and change it. By contrast, the GNU General Public
License is intended to guarantee your freedom to share and change free
software--to make sure the software is free for all its users. This
General Public License applies to most of the Free Software
Foundation's software and to any other program whose authors commit to
using it. (Some other Free Software Foundation software is covered by
the GNU Library General Public License instead.) You can apply it to
your programs, too.
When we speak of free software, we are referring to freedom, not
price. Our General Public Licenses are designed to make sure that you
have the freedom to distribute copies of free software (and charge for
this service if you wish), that you receive source code or can get it
if you want it, that you can change the software or use pieces of it
in new free programs; and that you know you can do these things.
To protect your rights, we need to make restrictions that forbid
anyone to deny you these rights or to ask you to surrender the rights.
These restrictions translate to certain responsibilities for you if you
distribute copies of the software, or if you modify it.
For example, if you distribute copies of such a program, whether
gratis or for a fee, you must give the recipients all the rights that
you have. You must make sure that they, too, receive or can get the
source code. And you must show them these terms so they know their
rights.
We protect your rights with two steps: (1) copyright the software, and
(2) offer you this license which gives you legal permission to copy,
distribute and/or modify the software.
Also, for each author's protection and ours, we want to make certain
that everyone understands that there is no warranty for this free
software. If the software is modified by someone else and passed on, we
want its recipients to know that what they have is not the original, so
that any problems introduced by others will not reflect on the original
authors' reputations.
Finally, any free program is threatened constantly by software
patents. We wish to avoid the danger that redistributors of a free
program will individually obtain patent licenses, in effect making the
program proprietary. To prevent this, we have made it clear that any
patent must be licensed for everyone's free use or not licensed at all.
The precise terms and conditions for copying, distribution and
modification follow.
GNU GENERAL PUBLIC LICENSE
TERMS AND CONDITIONS FOR COPYING, DISTRIBUTION AND MODIFICATION
0. This License applies to any program or other work which contains
a notice placed by the copyright holder saying it may be distributed
under the terms of this General Public License. The "Program", below,
refers to any such program or work, and a "work based on the Program"
means either the Program or any derivative work under copyright law:
that is to say, a work containing the Program or a portion of it,
either verbatim or with modifications and/or translated into another
language. (Hereinafter, translation is included without limitation in
the term "modification".) Each licensee is addressed as "you".
Activities other than copying, distribution and modification are not
covered by this License; they are outside its scope. The act of
running the Program is not restricted, and the output from the Program
is covered only if its contents constitute a work based on the
Program (independent of having been made by running the Program).
Whether that is true depends on what the Program does.
1. You may copy and distribute verbatim copies of the Program's
source code as you receive it, in any medium, provided that you
conspicuously and appropriately publish on each copy an appropriate
copyright notice and disclaimer of warranty; keep intact all the
notices that refer to this License and to the absence of any warranty;
and give any other recipients of the Program a copy of this License
along with the Program.
You may charge a fee for the physical act of transferring a copy, and
you may at your option offer warranty protection in exchange for a fee.
2. You may modify your copy or copies of the Program or any portion
of it, thus forming a work based on the Program, and copy and
distribute such modifications or work under the terms of Section 1
above, provided that you also meet all of these conditions:
a) You must cause the modified files to carry prominent notices
stating that you changed the files and the date of any change.
b) You must cause any work that you distribute or publish, that in
whole or in part contains or is derived from the Program or any
part thereof, to be licensed as a whole at no charge to all third
parties under the terms of this License.
c) If the modified program normally reads commands interactively
when run, you must cause it, when started running for such
interactive use in the most ordinary way, to print or display an
announcement including an appropriate copyright notice and a
notice that there is no warranty (or else, saying that you provide
a warranty) and that users may redistribute the program under
these conditions, and telling the user how to view a copy of this
License. (Exception: if the Program itself is interactive but
does not normally print such an announcement, your work based on
the Program is not required to print an announcement.)
These requirements apply to the modified work as a whole. If
identifiable sections of that work are not derived from the Program,
and can be reasonably considered independent and separate works in
themselves, then this License, and its terms, do not apply to those
sections when you distribute them as separate works. But when you
distribute the same sections as part of a whole which is a work based
on the Program, the distribution of the whole must be on the terms of
this License, whose permissions for other licensees extend to the
entire whole, and thus to each and every part regardless of who wrote it.
Thus, it is not the intent of this section to claim rights or contest
your rights to work written entirely by you; rather, the intent is to
exercise the right to control the distribution of derivative or
collective works based on the Program.
In addition, mere aggregation of another work not based on the Program
with the Program (or with a work based on the Program) on a volume of
a storage or distribution medium does not bring the other work under
the scope of this License.
3. You may copy and distribute the Program (or a work based on it,
under Section 2) in object code or executable form under the terms of
Sections 1 and 2 above provided that you also do one of the following:
a) Accompany it with the complete corresponding machine-readable
source code, which must be distributed under the terms of Sections
1 and 2 above on a medium customarily used for software interchange; or,
b) Accompany it with a written offer, valid for at least three
years, to give any third party, for a charge no more than your
cost of physically performing source distribution, a complete
machine-readable copy of the corresponding source code, to be
distributed under the terms of Sections 1 and 2 above on a medium
customarily used for software interchange; or,
c) Accompany it with the information you received as to the offer
to distribute corresponding source code. (This alternative is
allowed only for noncommercial distribution and only if you
received the program in object code or executable form with such
an offer, in accord with Subsection b above.)
The source code for a work means the preferred form of the work for
making modifications to it. For an executable work, complete source
code means all the source code for all modules it contains, plus any
associated interface definition files, plus the scripts used to
control compilation and installation of the executable. However, as a
special exception, the source code distributed need not include
anything that is normally distributed (in either source or binary
form) with the major components (compiler, kernel, and so on) of the
operating system on which the executable runs, unless that component
itself accompanies the executable.
If distribution of executable or object code is made by offering
access to copy from a designated place, then offering equivalent
access to copy the source code from the same place counts as
distribution of the source code, even though third parties are not
compelled to copy the source along with the object code.
4. You may not copy, modify, sublicense, or distribute the Program
except as expressly provided under this License. Any attempt
otherwise to copy, modify, sublicense or distribute the Program is
void, and will automatically terminate your rights under this License.
However, parties who have received copies, or rights, from you under
this License will not have their licenses terminated so long as such
parties remain in full compliance.
5. You are not required to accept this License, since you have not
signed it. However, nothing else grants you permission to modify or
distribute the Program or its derivative works. These actions are
prohibited by law if you do not accept this License. Therefore, by
modifying or distributing the Program (or any work based on the
Program), you indicate your acceptance of this License to do so, and
all its terms and conditions for copying, distributing or modifying
the Program or works based on it.
6. Each time you redistribute the Program (or any work based on the
Program), the recipient automatically receives a license from the
original licensor to copy, distribute or modify the Program subject to
these terms and conditions. You may not impose any further
restrictions on the recipients' exercise of the rights granted herein.
You are not responsible for enforcing compliance by third parties to
this License.
7. If, as a consequence of a court judgment or allegation of patent
infringement or for any other reason (not limited to patent issues),
conditions are imposed on you (whether by court order, agreement or
otherwise) that contradict the conditions of this License, they do not
excuse you from the conditions of this License. If you cannot
distribute so as to satisfy simultaneously your obligations under this
License and any other pertinent obligations, then as a consequence you
may not distribute the Program at all. For example, if a patent
license would not permit royalty-free redistribution of the Program by
all those who receive copies directly or indirectly through you, then
the only way you could satisfy both it and this License would be to
refrain entirely from distribution of the Program.
If any portion of this section is held invalid or unenforceable under
any particular circumstance, the balance of the section is intended to
apply and the section as a whole is intended to apply in other
circumstances.
It is not the purpose of this section to induce you to infringe any
patents or other property right claims or to contest validity of any
such claims; this section has the sole purpose of protecting the
integrity of the free software distribution system, which is
implemented by public license practices. Many people have made
generous contributions to the wide range of software distributed
through that system in reliance on consistent application of that
system; it is up to the author/donor to decide if he or she is willing
to distribute software through any other system and a licensee cannot
impose that choice.
This section is intended to make thoroughly clear what is believed to
be a consequence of the rest of this License.
8. If the distribution and/or use of the Program is restricted in
certain countries either by patents or by copyrighted interfaces, the
original copyright holder who places the Program under this License
may add an explicit geographical distribution limitation excluding
those countries, so that distribution is permitted only in or among
countries not thus excluded. In such case, this License incorporates
the limitation as if written in the body of this License.
9. The Free Software Foundation may publish revised and/or new versions
of the General Public License from time to time. Such new versions will
be similar in spirit to the present version, but may differ in detail to
address new problems or concerns.
Each version is given a distinguishing version number. If the Program
specifies a version number of this License which applies to it and "any
later version", you have the option of following the terms and conditions
either of that version or of any later version published by the Free
Software Foundation. If the Program does not specify a version number of
this License, you may choose any version ever published by the Free Software
Foundation.
10. If you wish to incorporate parts of the Program into other free
programs whose distribution conditions are different, write to the author
to ask for permission. For software which is copyrighted by the Free
Software Foundation, write to the Free Software Foundation; we sometimes
make exceptions for this. Our decision will be guided by the two goals
of preserving the free status of all derivatives of our free software and
of promoting the sharing and reuse of software generally.
NO WARRANTY
11. BECAUSE THE PROGRAM IS LICENSED FREE OF CHARGE, THERE IS NO WARRANTY
FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE LAW. EXCEPT WHEN
OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES
PROVIDE THE PROGRAM "AS IS" WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED
OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS
TO THE QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE
PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING,
REPAIR OR CORRECTION.
12. IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING
WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MAY MODIFY AND/OR
REDISTRIBUTE THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES,
INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING
OUT OF THE USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED
TO LOSS OF DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY
YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER
PROGRAMS), EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE
POSSIBILITY OF SUCH DAMAGES.
END OF TERMS AND CONDITIONS
How to Apply These Terms to Your New Programs
If you develop a new program, and you want it to be of the greatest
possible use to the public, the best way to achieve this is to make it
free software which everyone can redistribute and change under these terms.
To do so, attach the following notices to the program. It is safest
to attach them to the start of each source file to most effectively
convey the exclusion of warranty; and each file should have at least
the "copyright" line and a pointer to where the full notice is found.
<one line to give the program's name and a brief idea of what it does.>
Copyright (C) <year> <name of author>
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA
Also add information on how to contact you by electronic and paper mail.
If the program is interactive, make it output a short notice like this
when it starts in an interactive mode:
Gnomovision version 69, Copyright (C) year name of author
Gnomovision comes with ABSOLUTELY NO WARRANTY; for details type `show w'.
This is free software, and you are welcome to redistribute it
under certain conditions; type `show c' for details.
The hypothetical commands `show w' and `show c' should show the appropriate
parts of the General Public License. Of course, the commands you use may
be called something other than `show w' and `show c'; they could even be
mouse-clicks or menu items--whatever suits your program.
You should also get your employer (if you work as a programmer) or your
school, if any, to sign a "copyright disclaimer" for the program, if
necessary. Here is a sample; alter the names:
Yoyodyne, Inc., hereby disclaims all copyright interest in the program
`Gnomovision' (which makes passes at compilers) written by James Hacker.
<signature of Ty Coon>, 1 April 1989
Ty Coon, President of Vice
This General Public License does not permit incorporating your program into
proprietary programs. If your program is a subroutine library, you may
consider it more useful to permit linking proprietary applications with the
library. If this is what you want to do, use the GNU Library General
Public License instead of this License.
Next: Metasyntactic variable index, Previous: License, Up: Top [Contents][Index]
| Jump to: | .
A B C D E F G H I J K L M N O P Q R S T U V W |
|---|
| Jump to: | .
A B C D E F G H I J K L M N O P Q R S T U V W |
|---|
Next: Syntax index, Previous: Concept index, Up: Top [Contents][Index]
| Jump to: | .
:
<
|
A B C E F G I J L M O P Q R S T V |
|---|
| Jump to: | .
:
<
|
A B C E F G I J L M O P Q R S T V |
|---|
Previous: Metasyntactic variable index, Up: Top [Contents][Index]
| Jump to: | !
#
$
%
&
(
*
+
-
/
0
1
2
3
<
=
>
?
^
|
~
A B C D E F G H I J L M N O P Q R S T U V W X Y Z |
|---|
| Jump to: | !
#
$
%
&
(
*
+
-
/
0
1
2
3
<
=
>
?
^
|
~
A B C D E F G H I J L M N O P Q R S T U V W X Y Z |
|---|
If you are looking for a graphical front-end to GetDP, you may consider using Gmsh (available at http://gmsh.info). Gmsh permits to construct geometries, generate meshes, launch computations and visualize results directly from within a user-friendly graphical interface. The file formats used by Gmsh for mesh generation and post-processing are the default file formats accepted by GetDP (see Input file format, and Types for PostOperation).